電験一種 H28年 理論 問4
次の文章は, 電界内での電子の動きに関する記述である。文中の(0) に当てはまる最も適切なものを解答群の中から選べ。なお, 電子の質量を \(m_0\), 電荷量を \(-e\) とする。ただし, 電子の速度は電子の質量 \(m_0\) が変化しない範囲とする。
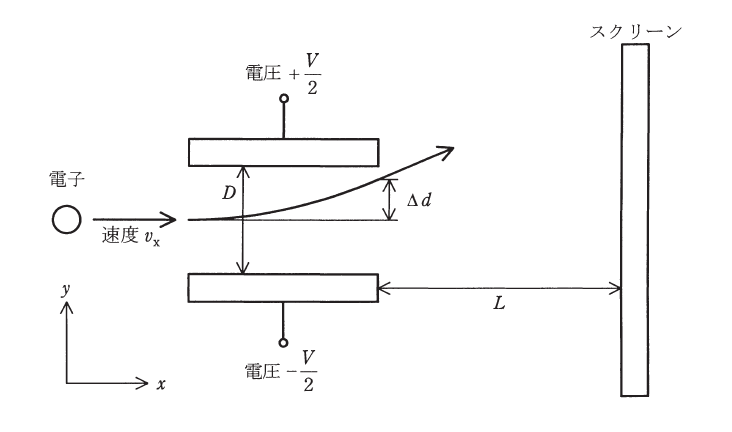
図のように, 真空中に置かれ, 上側に \(+\dfrac{V}{2}\), 下側に \(-\dfrac{V}{2}\) の電圧を印加した平行二枚板電極がある。その間隔は \(D\) である。この平行二枚板電極の中央に, 横方向から \(x\) 方向の速度 \(v_x\) のみの速度をもつ電子を入射したところ, 図のように平行二枚板電極間を通過した。平行二枚板電極間の電界は端部においても一様とすると, 平行二枚板電極間を通過する時間 \(t_1\) の間だけ, 一定電界により上側(\( y \)方向)への力 (1) を受ける。このときの電子の加速度は \(\dfrac{\mathrm{d}^2 y}{\mathrm{d}t^2} \)であるから、電子の\(y\)方向に関する運動方程式を立てれば, \(\dfrac{\mathrm{d}^2 y}{\mathrm{d}t^2} = \)(2) である微分方程式が得られる。平行二枚板電極間を通過した直後の \(y\) 方向の変位を \(\Delta d\),\(y\) 方向の速度を \(v_y\)とすると, \(y\) 方向の初期速度が零であることに注意して, 時間 \(t_1\) と変位 \(\Delta d\) の間には \(\Delta d = \) (3) の関係があり, 同様に \(v_y\) を \(t_1\) を用いて表してから \(\Delta d\) の式を用い \(t_1\) を消去すると, \(v_y = \) (4) が得られる。
このあと, 電子は等速度で運動し続けるので, 平行二枚板電極から\(x\)方向に\(L\)だけ離れた位置の\(yz\)平面にスクリーンを置くと, 平行二枚板電極間を通り過ぎた後からスクリーンにたどり着くまでの\(y\)方向への変位は(5) である。
| (イ) | \(\displaystyle \sqrt{\frac{2eV}{m_0}}\) | (ロ)(3) | \(\displaystyle \frac{eVt_1^2}{2m_0 D}\) | (ハ) | \(\displaystyle \frac{eVt_1^2}{m_0 D}\) | (ニ) | \(\displaystyle \frac{v_x }{v_y}L\) |
| (ホ) | \(\displaystyle \frac{eVD}{m_0}\) | (ヘ) | \(eV D\) | (ト)(4) | \(\displaystyle \sqrt{\frac{2eV\Delta d}{m_0 D}}\) | (チ) | \(\displaystyle \frac{eV}{m_0}\) |
| (リ)(5) | \(\displaystyle \frac{v_y }{v_x}L\) | (ヌ) | \(eV\) | (ル)(2) | \(\displaystyle \frac{eV}{m_0 D}\) | (ヲ) | \(\displaystyle \sqrt{\frac{2eV}{m_0}} \frac{L}{v_x}\) |
| (ワ) | \(\displaystyle \frac{eVt_1}{m_0 D}\) | (カ) | \(\displaystyle \sqrt{\frac{eV\Delta d}{m_0 D}}\) | (ヨ)(1) | \(\displaystyle \frac{eV}{D}\) |
出典:平成28年度第一種電気主任技術者理論科目A問題問4
解説
基本的な問題であり確実に解けるようにしておきたいところです。
電子が受ける\(y\)方向への力
電子が受ける力\(F\)の大きさは電荷量と電界の積であり、電界\(E\)は\(\dfrac{V}{D}\)で表されるので
\begin{aligned} F &= eE \\ &= \dfrac{eV}{D}\\ \end{aligned}
よって答えは(ヨ)の\(\displaystyle \frac{eV}{D}\)です。
電子に関する微分方程式
電子の受ける力は電子の質量と加速度\(a\)の積で表されます。加速度は位置の時間についての二階微分であり、これは(1)の力と等しいため、これらを整理すると
\begin{aligned} m_0 a &= \dfrac{eV}{D} \\ m_0 \frac{ \mathrm{d} ^2 y }{\mathrm{d} t^2} &= \dfrac{eV}{D} \\ \frac{ \mathrm{d} ^2 y }{\mathrm{d} t^2} &= \dfrac{eV}{m_0 D} \\ \end{aligned}
となりますので、答えは(ル)の\(\displaystyle \frac{eV}{m_0 D}\)です。
時間\(t_1\)と変異\(\Delta d\)の関係
(2)の式を計算して変位を求めます。
速度は加速度を時間で積分したものですから
\begin{aligned} \int \frac{d^2y}{dt^2} dt &= \int \frac{eV}{m_0D} dt \\ \frac{dy}{dt} &= \frac{eV}{m_0D} t + C_1 \quad (C_1は積分定数)\\ \end{aligned}
問題より、初速度は0であることから\(C_1 = 0\)なので、時刻\(t\)における速度\(v\)は
\begin{aligned} v &= \frac{eV}{m_0D} t \\ \end{aligned}
となります。変位はこれを時間で積分したものなので、
\begin{aligned} \int \frac{dy}{dt} dt &= \int \frac{eV}{m_0D} dt \\ y &= \frac{1}{2} \cdot \frac{eV}{m_0D} t^2 + C_2 \quad (C_2は積分定数) \end{aligned}
時刻\(t_1\)における変位\(\Delta d\)は、変位であることから初期位置\(C_2\)は0なことから
\begin{aligned} \Delta d &= \frac{eV t_1^2}{2m_0D} \\ \end{aligned}
となりますので、答えは(ロ)の\(\displaystyle \frac{eVt_1^2}{2m_0 D}\)です。
速度\(v_y\)
(3)の途中で求めた\(v\)に\(t=t_1\)を代入して\(v_y\)を求めます。
\begin{aligned} v_y &= \frac{eV}{m_0D} t_1 \\ \end{aligned}
(3)の答えより\(t_1\)を求めます。
\begin{aligned} \Delta d &= \frac{eV t_1^2}{2m_0D} \\ t_1^2 &= \frac{2m_0D \Delta d}{eV} \\ t_1 &= \sqrt{ \frac{2m_0D \Delta d}{eV}} \\ \end{aligned}
下の式を上の式に代入し\(t_1\)を消去します。
\begin{aligned} v_y &= \frac{eV}{m_0D} \cdot \sqrt{ \frac{2m_0D \Delta d}{eV}} \\ &= \sqrt{ \frac{2 eV \Delta d}{m_0D}} \\ \end{aligned}
よって答えは(ト)の\(\displaystyle \sqrt{\frac{2eV\Delta d}{m_0 D}}\)です。
スクリーンにたどり着くまでの\(y\)方向への変位
平行二枚板電極を通り過ぎた後、電子は\(x\)方向には速度\(v_x\)、\(y\)方向には速度\(v_y\)で等速度で運動します。
スクリーンまでの距離が\(L\)なので、電子がスクリーンに着くまでの時間\(t_2\)は\(\dfrac{L}{v_x}\)です。
その時の\(y\)方向の変位は\(v_y t_2\)で表されますので、これらより
\begin{aligned} v_y t_2 &= \dfrac{v_y }{v_x} L \\ \end{aligned}
となりますので、答えは(リ)の\(\displaystyle \frac{v_y }{v_x}L\)です。
- (1)ヨ \(\displaystyle \frac{eV}{D}\)
- (2)ル \(\displaystyle \frac{eV}{m_0 D}\)
- (3)ロ \(\displaystyle \frac{eVt_1^2}{2m_0 D}\)
- (4)ト \(\displaystyle \sqrt{\frac{2eV\Delta d}{m_0 D}}\)
- (5)リ \(\displaystyle \frac{v_y }{v_x}L\)