電験一種 H28年 理論 問3
次の文章は、直流回路の合成抵抗に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
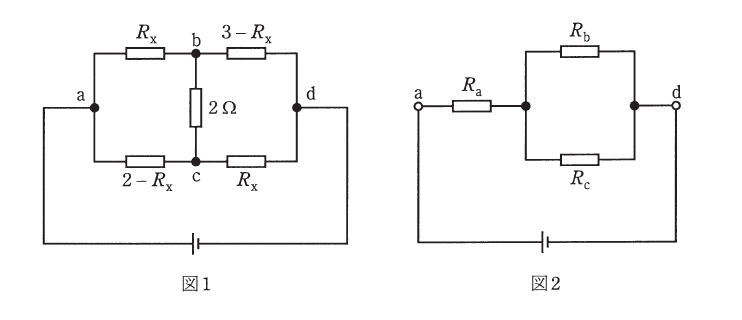
図1に示す回路の合成抵抗を求めたい。まず、節点a-b-cからなる\(\Delta\)接続部分に「\(\Delta\)-Y変換」を施すと、図1のa-d間の抵抗は図2のように表すことができる。
図2の\(R_a\), \(R_b\), \(R_c\)は、\(R_x\)を用いて\(R_a = \)(1) [Ω], \(R_b = \)(2) [Ω], \(R_c = \)(3) [Ω]となる。
したがって、回路全体の合成抵抗\(R_{ad}\)は\(R_{ad} = \)(4) [Ω]と表され、\(R_x = \)(5) Ωにおいて最大となる。
| (イ) | \(\displaystyle \frac{R_x+6}{2}\) | (ロ)(3) | \(\displaystyle \frac{R_x+2}{2}\) | (ハ)(1) | \(\displaystyle \frac{-R_x^2+2R_x}{4}\) |
| (ニ) | \(\displaystyle \frac{-R_x+2}{2}\) | (ホ) | \(0.5\) | (ヘ)(5) | \(1.2\) |
| (ト) | \(\displaystyle \frac{-R_x+3}{4}\) | (チ) | \(\displaystyle \frac{R_x^2}{2}\) | (リ) | \(2\) |
| (ヌ)(4) | \(\displaystyle \frac{-5R_x^2+12R_x+12}{16}\) | (ル) | \(\displaystyle \frac{R_x+2}{4}\) | (ヲ) | \(\displaystyle \frac{R_x^2}{R_x+1}\) |
| (ワ)(2) | \(\displaystyle \frac{-R_x+6}{2}\) | (カ) | \(\displaystyle \frac{11R_x^2+44R_x+12}{4}\) | (ヨ) | \(\displaystyle \frac{11R_x^2+12R_x+12}{4}\) |
出典:平成28年度第一種電気主任技術者理論科目A問題問3
解説
Δ-Y変換が分かっていれば難しくはありませんが、計算に時間を要するかもしれません。
抵抗\(R_a\)
Δ-Y変換の公式に従いabcのΔをYに変換します。
参考:実践的な複素数計算法(3)ΔーY変換による回路の簡単化 | 音声付き電気技術解説講座 | 公益社団法人 日本電気技術者協会
\begin{aligned} R_a &= \frac{R_x (2 - R_x)}{R_x + 2 + (2 - R_x)} \\ &= \frac{-R_x^2 + 2R_x}{4} \end{aligned}
よって答えは(ハ)の\(\displaystyle \frac{-R_x^2+2R_x}{4}\)です。
抵抗\(R_b\)
同様にΔ-Y変換するだけですが、\(R_b\)は\(3-R_x\)との和になることだけに注意が必要です。
\begin{aligned} R_b &= \frac{2R_x }{R_x + 2 + (2 - R_x)} + 3 - R_x \\ &= \frac{R_x}{2} + 3 - R_x \\ &= \frac{-R_x + 6}{2} \end{aligned}
よって答えは(ワ)の\(\displaystyle \frac{-R_x+6}{2}\)です。
抵抗\(R_c\)
(2)と同様に計算します。
\begin{aligned} R_c &= \frac{2(2 - R_x)}{R_x + 2 + (2 - R_x)} + R_x \\ &= \frac{-R_x + 2}{2} + R_x \\ &= \frac{R_x + 2}{2} \end{aligned}
よって答えは(ロ)の\(\displaystyle \frac{R_x+2}{2}\)です。
回路全体の合成抵抗
回路全体の合成抵抗は\(R_b\)と\(R_c\)の並列接続と、\(R_a\)の和になるため
\begin{aligned} R_{ad} &= R_a + \frac{R_b R_c}{R_b + R_c} \\ &= \frac{-R_x^2 + 2R_x}{4} + \frac{\dfrac{-R_x + 6}{2} \times \dfrac{R_x + 2}{2}}{\dfrac{-R_x + 6}{2} + \dfrac{R_x + 2}{2}} \\ &= \frac{-R_x^2 + 2R_x}{4} + \frac{-R_x^2 + 4R_x + 12}{16} \\ &= \frac{-5R_x^2 + 12R_x + 12}{16} \end{aligned}
よって答えは(ヌ)の\(\displaystyle \frac{-5R_x^2+12R_x+12}{16}\)です。
回路全体の合成抵抗を最大にする\(R_x\)
微分して\( \dfrac{\mathrm {d} R_{ad}}{\mathrm {d} R_x} = 0 \)となる時の\(R_x\)を調べます。
(2)より磁束密度\(B_z = 2k\)であり、また問題に書いてある通り内部の磁束密度は\(\mu_0 J\)で一様なので
\begin{aligned} \dfrac{\mathrm {d} R_{ad}}{\mathrm {d} R_x} &= \frac{-10R_x + 12}{16} \\ 0 &= \frac{-10R_x + 12}{16} \\ R_x &= 1.2 \\ \end{aligned}
\( \dfrac{\mathrm {d}^2 R_{ad}}{\mathrm {d} R_x^2} \lt 0 \)なのでこの時の\(R_x\)は極大値です。よって答えは(ヘ)の\(1.2\)です。
- (1)ハ \(\displaystyle \frac{-R_x^2+2R_x}{4}\)
- (2)ワ \(\displaystyle \frac{-R_x+6}{2}\)
- (3)ロ \(\displaystyle \frac{R_x+2}{2}\)
- (4)ヌ \(\displaystyle \frac{-5R_x^2+12R_x+12}{16}\)
- (5)ヘ \(1.2\)