電験一種 H28年 理論 問2
次の文章は、ベクトルポテンシャル、磁界及び電流に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
なお、ベクトルポテンシャルとは磁束密度\(\boldsymbol{B}\)に対して\(\boldsymbol{B} = \nabla \times \boldsymbol{A}\)を満たすベクトル\(\boldsymbol{A}\)のことであり、円筒座標系では、
\[ \begin{pmatrix} B_r \\ B_{\theta} \\ B_z \end{pmatrix} = \nabla \times \begin{pmatrix} A_r \\ A_{\theta} \\ A_z \end{pmatrix} = \begin{pmatrix} \dfrac{1}{r} \dfrac{\partial A_z}{\partial \theta} - \dfrac{\partial A_\theta}{\partial z} \\ \dfrac{\partial A_r}{\partial z} - \dfrac{\partial A_z}{\partial r} \\ \dfrac{1}{r} \dfrac{\partial (r A_\theta)}{\partial r} - \dfrac{1}{r} \dfrac{\partial A_r}{\partial \theta} \end{pmatrix} \]
と与えられる。
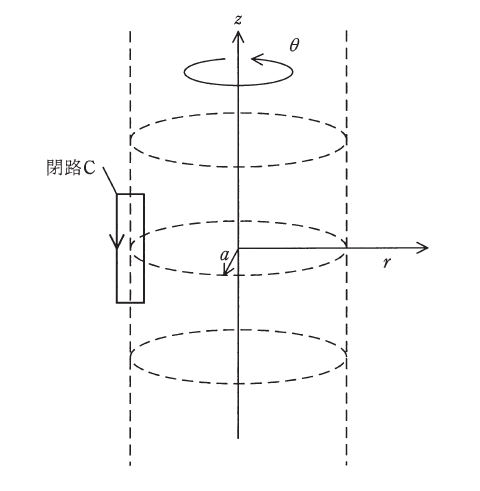
図のような円筒座標系において、以下の①式及び②式のように半径\(r\)の関数として定義されたベクトルポテンシャル\(\boldsymbol{A}\)を考える。なお、\(k\)は定数であり、\(\mu_0\)は真空の透磁率である。
\(A_r(r, \theta, z) = A_z(r, \theta, z) = 0 \cdots ① \)
\(A_\theta(r, \theta, z) = \begin{cases} kr & (r \leqq a) \\ \dfrac{ka^2}{r} & (r > a) \end{cases} \cdots ② \)
\(r < a\)における磁束密度は、
\(B_r = 0, B_\theta = \)(1)\(, B_z = \)(2)
\(r > a\)における磁束密度は、
\(B_r = 0, B_\theta = \)(1)\(, B_z = \)(1)
となる。
次に、このような磁場分布を形成する電流を考える。図中の閉路\(C\)についてアンペールの法則を適用すると、電流は\(r=a\)の円筒面を(3)方向に流れていることになり、上記の分布は(4)に流れる電流が作り出す磁界を表していることが分かる。
\(z\)方向単位長さ当たりの電流密度が\(J\)である(4)に流れる電流の内部には磁束密度\(\mu_0 J\)の一様な磁界が形成されることから、ベクトルポテンシャル\(\boldsymbol{A}\)は\(z\)方向単位長さ当たりの電流密度(5)の(3)方向電流によって形成されていることが分かる。
| (イ) | \(\displaystyle \frac{1}{k}\) | (ロ)(3) | \(\theta\) | (ハ)(5) | \(\displaystyle \frac{2k}{\mu_0}\) |
| (ニ) | 直線状 | (ホ) | \(\mu_0 k\) | (ヘ) | \(r\) |
| (ト)(2) | \(2k\) | (チ) | \(k\) | (リ) | \(\displaystyle \frac{k}{r}\) |
| (ヌ) | \(\displaystyle \frac{k}{r^2}\) | (ル)(4) | 無限長直線状ソレノイド | (ヲ) | \(\displaystyle \frac{k}{2\pi\mu_0}\) |
| (ワ)(1) | \(0\) | (カ) | 円環状ソレノイド | (ヨ) | \(z\) |
出典:平成28年度第一種電気主任技術者理論科目A問題問2
解説
一見難しそうに見えますが実際解くと実は難しくない問題です。このような問題はたまにあるため本番でも冷静に考えられるようにしたいところです。
磁束密度\(B_\theta \)
問題文で式が与えられていますので、その通り計算します。
\begin{aligned} B_{\theta} &= \dfrac{\partial A_r}{\partial z} - \dfrac{\partial A_z}{\partial r} \\ &= 0 \end{aligned}
\(A_r\)と\(A_z\)は0なので当然0です。よって答えは(ワ)の\(0\)です。
磁束密度\(B_z \)
(1)と同様に計算します。(2)で求める磁束密度は\( r \lt a \)のときなので
\begin{aligned} B_z &= \dfrac{1}{r} \dfrac{\partial (r A_\theta)}{\partial r} - \dfrac{1}{r} \dfrac{\partial A_r}{\partial \theta} \\ &= \dfrac{1}{r} \dfrac{\partial ( kr^2 )}{\partial r} - \dfrac{1}{r} \dfrac{\partial \left( 0 \right) }{\partial \theta} \\ &= 2k \end{aligned}
となり、答えは(ト)の\(2k\)です。
電流の流れる方向
(1)と(2)より、磁界はz方向のみに存在しその他の方向には存在しません。
よって、右ねじの法則より電流は\(\theta \)方向に流れていることが分かります。
答えは(ロ)の\(\theta\)です。
磁界分布を作り出す電流の形
(1)、(2)よりz方向の磁界は\( r \lt a \)の時\(2k\)で\( r \gt a \)の時は0です。
外部の磁界が0なので、これは(ル)の無限長直線状ソレノイドです。
なお、無限長でない場合は外部の磁束は0にはなりません。
電流密度
(2)より磁束密度\(B_z = 2k\)であり、また問題に書いてある通り内部の磁束密度は\(\mu_0 J\)で一様なので
\begin{aligned} 2k &= \mu_0 J \\ J &= \dfrac{2k}{\mu_0} \\ \end{aligned}
となりますので、答えは(ハ)の\(\displaystyle \frac{2k}{\mu_0}\)です。
- (1)ワ \(0\)
- (2)ト \(2k\)
- (3)ロ \(\theta\)
- (4)ル 無限長直線状ソレノイド
- (5)ハ \(\displaystyle \frac{2k}{\mu_0}\)