電験一種 H28年 理論 問1
次の文章は、三つの導体からなる同心球コンデンサに関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
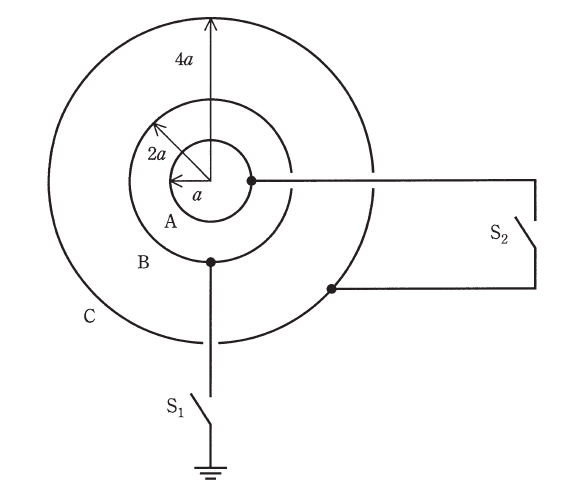
図のように、半径\(a\), \(2a\), \(4a\)の三つの導体球面A, B, Cが同心となるように真空中に置かれている。その厚さは無視できる。導体B及びCには穴が開けられてそこから導線が引き出されていて、スイッチ\(S_1\)を閉じると導体Bが接地され、スイッチ\(S_2\)を閉じると導体A及びCが短絡されるようになっている。
ただし、穴は十分小さく、かつ導線及びスイッチは周りの空間と絶縁されており、その影響は無視できるものとする。また、真空中の誘電率は\(\varepsilon_0\)とする。
最初に、スイッチ\(S_1\)及び\(S_2\)はともに開いており、導体Aには電荷\(Q\)が与えられている。このとき、無限遠を接地電位(零)としたときの導体Aの電位は(1)であり、静電容量は(2)である。また、導体Aより内側の空間における電界の大きさは(3)である。
次に、スイッチ\(S_1\)を閉じると十分時間が経ったとき、導体Aの電位は(4)になる。
さらに、スイッチ\(S_1\)を閉じたままスイッチ\(S_2\)も閉じて十分時間が経ったとき、導体Aに存在する電荷は(5)である。
| (イ) | \(\displaystyle \frac{Q}{16\pi\varepsilon_0 a}\) | (ロ) | \(\displaystyle \frac{1}{3}Q\) | (ハ)(2) | \(4\pi\varepsilon_0 a\) | (ニ)(3) | \(0\) |
| (ホ) | \(\displaystyle \frac{3Q}{8\pi\varepsilon_0 a}\) | (ヘ)(5) | \(\displaystyle \frac{1}{5}Q\) | (ト) | \(\displaystyle \frac{4}{3}\pi\varepsilon_0 a\) | (チ)(4) | \(\displaystyle \frac{Q}{8\pi\varepsilon_0 a}\) |
| (リ)(1) | \(\displaystyle \frac{Q}{4\pi\varepsilon_0 a}\) | (ヌ) | \(\displaystyle \frac{3Q}{4\pi\varepsilon_0 a}\) | (ル) | \(\displaystyle \frac{1}{4}Q\) | (ヲ) | \(\displaystyle \frac{16}{3}\pi\varepsilon_0 a\) |
| (ワ) | \(\displaystyle \frac{3Q}{4\pi\varepsilon_0 a^2}\) | (カ) | \(\displaystyle \frac{Q}{4\pi\varepsilon_0 a^2}\) | (ヨ) | \(\displaystyle \frac{3Q}{16\pi\varepsilon_0 a}\) |
出典:平成28年度第一種電気主任技術者理論科目A問題問1
解説
類題も多い一般的な問題です。
(5)は時間を要しますがそれ以外は過去問を繰り返せば解ける問題かと思います。
無限遠を接地電位(零)としたときの導体Aの電位
ガウスの法則より、導体Aの外部の電界\(E(r)\)は、中心に点電荷\(Q\)がある場合と同じように、以下の式で与えられます。
\(E(r) = \dfrac{Q}{4\pi\varepsilon_0 r^2}\)
ここで、rは球の中心からの距離、\(\varepsilon_0\)は真空中の誘電率です。
無限遠を接地電位(零)としたときの導体Aの電位\(V_A\)は、無限遠から導体Aの表面(r=a)まで電界を積分することで求められます。
\(\displaystyle V_A = -\int_{\infty}^{a} E(r) dr\)
電位の基準が無限遠で、電界の方向(正電荷から外向き)と積分の方向が逆なので、符号は負になります。
実際に計算した結果は以下のようになります。
\begin{aligned} V_A &= -\int_{\infty}^{a} \dfrac{Q}{4\pi\varepsilon_0 r^2} dr \\ &= -\dfrac{Q}{4\pi\varepsilon_0} \int_{\infty}^{a} \dfrac{1}{r^{2}} dr \\ &= -\dfrac{Q}{4\pi\varepsilon_0} \left[ -\dfrac{1}{r} \right] _{\infty}^{a} \\ &= \dfrac{Q}{4\pi\varepsilon_0 a} \\ \end{aligned}
よって答えは(リ)の\(\displaystyle \frac{Q}{4\pi\varepsilon_0 a}\)です。
その静電容量
静電容量\(C\)は\(C=\dfrac{Q}{V}\)で表されるので、(1)の\(V_A = \displaystyle \frac{Q}{4\pi\varepsilon_0 a} \)より、
\begin{aligned} C &= \dfrac{Q}{V_A} \\ &= 4\pi\varepsilon_0 a \\ \end{aligned}
となり、答えは(ハ)の\(4\pi\varepsilon_0 a\)です。
導体Aより内側の空間における電界の大きさ
導体Aは半径aの導体球面です。導体に電荷が与えられた場合、その電荷は導体の表面に分布します。内部には自由電荷は存在しません。
導体Aより内側の空間(\( r \lt a\))では、ガウス面内に電荷は存在しません。したがって、
\(\displaystyle \oint_S \vec{E} \cdot d\vec{S} = 0\)
これより、導体Aより内側の空間における電界の大きさEは0となります。
よって答えは(ニ)の\(0\)です。
スイッチ\(S_1\)を閉じ十分時間が経ったときの導体Aの電位
スイッチ\(S_1\)を閉じると、導体Bが接地されます。これは、導体Bの電位が零( \(V_B=0\) )になることを意味します。
このとき、導体Aには電荷Qが与えられたままです。
導体Bの電位が零になるためにはその内側の電荷の合計が0にならないといけないため、導体Bの内側表面に\(-Q\)の電荷が誘導されます。
導体Aの電位\(V_A\)は、導体Aから導体Bまで電界の積分と導体Bから無限遠までの電界の積分の和となります。ただし、導体Bは接地されているため、\(V_B=0\)です。
\begin{aligned} V_A &= -\int_{2a}^{a} E(r) dr + V_B \\ &= -\int_{2a}^{a} E(r) dr + 0 \\ &= -\int_{2a}^{a} \dfrac{Q}{4\pi\varepsilon_0 r^2} dr \\ &= -\dfrac{Q}{4\pi\varepsilon_0} \left[ -\dfrac{1}{r} \right]_{2a}^{a} \\ &= -\dfrac{Q}{4\pi\varepsilon_0} \left( -\dfrac{1}{a} + \dfrac{1}{2a} \right) \\ &= -\dfrac{Q}{4\pi\varepsilon_0} \left( -\dfrac{2}{2a} + \dfrac{1}{2a} \right) \\ &= -\dfrac{Q}{4\pi\varepsilon_0} \left( -\dfrac{1}{2a} \right) \\ &= \dfrac{Q}{8\pi\varepsilon_0 a} \\ \end{aligned}
よって答えは(チ)の\(\displaystyle \frac{Q}{8\pi\varepsilon_0 a}\)です。
スイッチ\(S_1\)を閉じたままスイッチ\(S_2\)も閉じて十分時間が経ったときの導体Aに存在する電荷
スイッチ\(S_2\)を閉じると導体Aの電荷Qの一部が導体Cに移動します。
各導体の電荷をそれぞれ\(Q_A\)、\(Q_B\)、\(Q_C\)とします。
ここで、外部との接続がないため電荷の合計はQのままなことから\(Q=Q_A+Q_C\)が成り立ちます。
また、スイッチ\(S_2\)を閉じていることにより導体Aと導体Cの電位は等しく(\(V_A = V_C\))なります。
また、\(\displaystyle V_A = -\int_{2a}^{a} \dfrac{Q_A}{4\pi\varepsilon_0 r^2} dr + V_B \)、\(\displaystyle V_B = -\int_{4a}^{2a} \dfrac{Q_A +Q_B}{4\pi\varepsilon_0 r^2} dr + V_C \)、\(\displaystyle V_C = -\int_{\infty}^{4a} \dfrac{Q_A +Q_B + Q_C}{4\pi\varepsilon_0 r^2} dr \)が成り立ちます。
\(V_B\)は接地されていることから0です。
これらをまとめると以下となります。
\begin{aligned} -\int_{2a}^{a} \dfrac{Q_A}{4\pi\varepsilon_0 r^2} dr &= -\int_{\infty}^{4a} \dfrac{Q_A +Q_B + Q_C}{4\pi\varepsilon_0 r^2} dr\\ \int_{4a}^{2a} \dfrac{Q_A +Q_B}{4\pi\varepsilon_0 r^2} dr &= -\int_{\infty}^{4a} \dfrac{Q_A +Q_B + Q_C}{4\pi\varepsilon_0 r^2} dr \\ Q &= Q_A+Q_C \\ \end{aligned}
これを解いていきます。まず1番目の式から解きます。
\begin{aligned} -\int_{2a}^{a} \frac{Q_A}{4\pi\varepsilon_0 r^2} dr &= -\int_{\infty}^{4a} \dfrac{Q_A +Q_B + Q_C}{4\pi\varepsilon_0 r^2} dr \\ -\frac{Q_A}{4\pi\varepsilon_0} \left[ -\frac{1}{r} \right]_{2a}^{a} &= -\frac{Q_A + Q_B + Q_C}{4\pi\varepsilon_0} \left[ -\frac{1}{r} \right]_{\infty}^{4a} \\ -\frac{Q_A}{4\pi\varepsilon_0} \left( -\frac{1}{2a} \right) &= -\frac{Q_A + Q_B + Q_C}{4\pi\varepsilon_0} \left( -\frac{1}{4a} - 0 \right) \\ \frac{Q_A}{8\pi\varepsilon_0 a} &= \frac{Q_A + Q_B + Q_C}{16\pi\varepsilon_0 a} \\ Q_A &= Q_B + Q_C \\ \end{aligned}
次に2番目の式を計算します。
\begin{aligned} \int_{4a}^{2a} \dfrac{Q_A +Q_B}{4\pi\varepsilon_0 r^2} dr &= -\int_{\infty}^{4a} \dfrac{Q_A +Q_B + Q_C}{4\pi\varepsilon_0 r^2} dr \\ \frac{Q_A + Q_B}{4\pi\varepsilon_0} \left[ -\frac{1}{r} \right]_{4a}^{2a} &= -\frac{Q_A + Q_B + Q_C}{4\pi\varepsilon_0} \left[ -\frac{1}{r} \right]_{\infty}^{4a} \\ \frac{Q_A + Q_B}{4\pi\varepsilon_0} \left( -\frac{1}{4a} \right) &= -\frac{Q_A + Q_B + Q_C}{4\pi\varepsilon_0} \left(- \frac{1}{4a} \right) \\ -Q_A - Q_B &= Q_A + Q_B + Q_C \\ 2Q_A + 2Q_B &= -Q_C \\ \end{aligned}
後はこれを解いて\(Q_B\)と\(Q_C\)を消去して\(Q_A\)を求めます。
\begin{cases} Q = Q_A + Q_C \quad & (1) \\ Q_A = Q_B + Q_C \quad & (2) \\ 2Q_A + 2Q_B = -Q_C \quad & (3) \end{cases}
\begin{aligned} Q_C &= -2Q_A - 2Q_B \\ \end{aligned} \begin{aligned} Q_A &= Q_B + (-2Q_A - 2Q_B) \\ Q_A &= Q_B - 2Q_A - 2Q_B \\ Q_A &= -Q_B - 2Q_A \\ 3Q_A &= -Q_B \\ Q_B &= -3Q_A \\ \end{aligned} \begin{aligned} Q_C &= -2Q_A - 2(-3Q_A) \\ Q_C &= 4Q_A \\ \end{aligned} \begin{aligned} Q &= Q_A + 4Q_A \\ Q_A &= \frac{Q}{5}\\ \end{aligned}
よって答えは(ヘ)の\(\displaystyle \frac{1}{5}Q\)です。
なお、他の電荷も求めると
\begin{aligned} Q_A &= \frac{1}{5}Q \\ Q_B &= -\frac{3}{5}Q \\ Q_C &= \frac{4}{5}Q \\ \end{aligned}
となります。
- (1)リ \(\displaystyle \frac{Q}{4\pi\varepsilon_0 a}\)
- (2)ハ \(4\pi\varepsilon_0 a\)
- (3)ニ \(0\)
- (4)チ \(\displaystyle \frac{Q}{8\pi\varepsilon_0 a}\)
- (5)ヘ \(\displaystyle \frac{1}{5}Q\)