電験一種 H27年 理論 問6
次の文章は, 分布定数回路に関する記述である。文中の(0) に当てはまる最も適切なものを解答群の中から選びなさい。
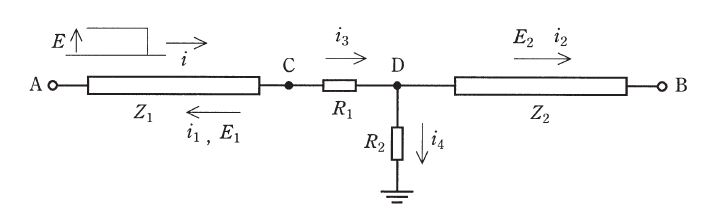
図のように, 特性インピーダンスがそれぞれ \(Z_1, Z_2\) の2本の無損失線路と抵抗が接続されている。線路間に電気的・磁気的結合はなく, また, A, Bそれぞれの端子では反射がないものとする。
A端子から接続点Cに向かって波頭が階段状で波高値 \(E\) の電圧波が進入したときについて考える。A 端子からの入射波による電流 \(i\), 接続点Cでの反射により生じる電圧 \(E_1\), 電流 \(i_1\), それぞれの抵抗に流れる電流 \(i_3, i_4\), \(Z_2\) 側への透過波による電圧 \(E_2\), 電流 \(i_2\) を図のようににとる。電流は入射波が接続点Cに向かって進行する方向及び透過波が接続点Dから離れる方向を正とする。
接続点Cの電圧, 電流の関係はそれぞれ次式で表される。
\(E+E_1 = \) (1) \(\cdots \text{①}\)
\(i+i_1 = i_3= i_2 +i_4 \cdots \text{②}\)
①式及び②式と, \(E_1 = -Z_1 i_1\) であることを考慮すれば, \(i_2 = \) (2) \(\times i_3\) となる。
ここで, 接続点CよりB側を見たインピーダンスを \(Z\) とすると,
\(E+E_1 = Zi_3 \cdots \text{③}\)
となる。\(i_1\)を\(i, Z_1, Z\)を用いて表すと,
\(i_1 = \) (3)
となる。\(E_2\)は\(E, Z_1, R_1, Z\)を用いて,
\(E_2 = \) (4)
となる。ここで \(E_1 = \dfrac{1}{2}E\) となるときの抵抗 \(R_1\) を \(Z_1, Z_2, R_2\) を用いて表すと,\(R_1 = \) (5) となる。
\(i_1, E_1\)は反射波のみとする。
電流はA\(\to\)C, C\(\to\)B, D\(\to\)接地の向きを正とする。
| (イ) | \(\displaystyle \frac{2(Z_1-R_1)}{Z_1-Z}E\) | (ロ) | \(\displaystyle \frac{Z_1+Z}{Z-Z_1}i\) | (ハ)(1) | \(R_1i_3+E_2\) |
| (ニ) | \(\displaystyle \frac{Z_2}{R_2+Z_2}\) | (ホ) | \(\displaystyle \frac{Z_1+Z}{Z_1-Z}i\) | (ヘ)(3) | \(\displaystyle \frac{Z_1-Z}{Z_1+Z}i\) |
| (ト)(2) | \(\displaystyle \frac{R_2}{R_2+Z_2}\) | (チ) | \(\displaystyle \frac{1}{3}Z_1-\frac{R_2Z_2}{R_2+Z_2}\) | (リ) | \(\displaystyle \frac{2(Z-R_1)}{Z-Z_1}E\) |
| (ヌ) | \(E_2\) | (ル) | \(R_1i_3\) | (ヲ)(4) | \(\displaystyle \frac{2(Z-R_1)}{Z_1+Z}E\) |
| (ワ) | \(\displaystyle Z_1-\frac{R_2Z_2}{3(R_2+Z_2)}\) | (カ) | \(\displaystyle \frac{Z_2}{R_1+Z_2}\) | (ヨ)(5) | \(\displaystyle 3Z_1-\frac{R_2Z_2}{R_2+Z_2}\) |
出典:平成27年度第一種電気主任技術者理論科目B問題問6
解説
分布定数回路は二次試験の電力・管理でも出てくる内容でありしっかり理解するだけの価値はあります。
接続点Cの電圧
接続点\(C\)からB側を見た時の電圧は\(R_1 i_3 + E_2\)なので答えは(ハ)の\(R_1i_3+E_2\)です。
なお、電圧は方向を意識しないため接続点Cの電圧は\(E+E_1\)となります。
\(i_2\)を\(i_3\)で表す
接続点Dの電圧は\(E_2 = Z_2 i_2\)なので、\(R_2\)の抵抗に注目すると以下が成り立ちます。
\begin{aligned} i_4 &= \dfrac{E_2}{R_2} \\ &= \dfrac{Z_2}{R_2} i_2 \\ \end{aligned}
これを問題文にある式\(i_3 = i_2 + i_4\)に代入します。
\begin{aligned} i_3 &= i_2 + i_4 \\ &= i_2 + \dfrac{Z_2}{R_2} i_2 \\ &= \left( 1 + \dfrac{Z_2}{R_2} \right) i_2 \\ \end{aligned}
\begin{aligned} i_2 &= \frac{R_2}{R_2+Z_2} i_3 \\ \end{aligned}
よって答えは(ト)の\(\displaystyle \frac{R_2}{R_2+Z_2}\)です。
※ここ分流の法則だけで解けるので\(E_1 = -Z_1 i_1\)であることを考慮することの意味がいまいち分かりませんでした
\(i_1\)を\(i\)、\(Z_1\)、\(Z\)を用いて表す
\(i+i_1 = i_3\)、\(E = Z_1 i \)、\(E_1 = -Z_1 i_1\)を使用して整理します。
\begin{aligned} E + E_1 &= Zi_3 \\ Z_1 i -Z_1 i_1 &= Z\left( i+i_1 \right) \\ \left( Z_1 + Z \right) i_1 &= \left( Z_1 - Z \right) i \\ i_1 &= \dfrac{ Z_1 - Z }{ Z_1 + Z } i \\ \end{aligned}
よって答えは(ヘ)の\(\displaystyle \frac{Z_1-Z}{Z_1+Z}i\)です。
なお、この問題は\(i\)と\(i_3\)の関係を求める、つまり電流反射係数を出せばいいので、
電圧反射係数\(\dfrac{ Z - Z_1 }{ Z + Z_1 } \)、\(Z\)が\(0\)の時に-1、\(Z\)が\(\infty\)の時に1になるということを覚えておけば、電流の時はこの符号を逆にすればいいのでそこからも判断できます。
\(E_2\)を\(E\)、\(Z_1\)、\(R_1\)、\(Z\)を用いて表す
(1)の\(E+E_1 = R_1 i_3+E_2\)と\(E+E_1 = Zi_3\)から\(E_2\)について整理していきます。
\begin{aligned} E+E_1 &= R_1 i_3+E_2 \\ Zi_3 &= R_1 i_3+E_2 \\ E_2 &= Zi_3 - R_1 i_3 \\ E_2 &= \left( Z - R_1\right) i_3 \\ \end{aligned}
また、\(i_3= i+i_1\)、(3)より\( i_1 = \dfrac{ Z_1 - Z }{ Z_1 + Z } i \)なので
\begin{aligned} i_3 &= i+i_1 \\ i_3 &= i + \dfrac{ Z_1 - Z }{ Z_1 + Z } i \\ i_3 &= \dfrac{ 2Z_1 }{ Z_1 + Z } i \\ i_3 &= \dfrac{ 2E }{ Z_1 + Z } \\ \end{aligned}
これを代入しますと
\begin{aligned} E_2 &= \left( Z - R_1\right) i_3 \\ E_2 &= \left( Z - R_1\right) \dfrac{ 2E }{ Z_1 + Z } \\ E_2 &= \dfrac{ 2 \left( Z - R_1\right)}{ Z_1 + Z } E\\ \end{aligned}
となりますので、答えは(ヲ)の\(\displaystyle \frac{2(Z-R_1)}{Z_1+Z}E\)です。
なお、この問題は選択肢的には(イ)、(リ)、(ヲ)が候補になるかと思いますが、(イ)と(リ)は\(Z=Z_1\)の時に分母が0になります。A点からC点のインピーダンスとC点からB側のインピーダンスが同じだと\(E_2\)が\(\infty\)になるというのは感覚的におかしいです。
そのため、これらは選択肢から外せますので消去法で(ヲ)を導くことも可能です。
\(E_1 = \dfrac{1}{2} E\)となるときの抵抗\(R_1\)を\(Z_1\)、\(Z_2\)、\(R_2\)を用いて表す
\(E_1\)が\(\dfrac{1}{2}E\)になるということは電圧反射係数が\(\dfrac{1}{2}\)ということなので、そこから求めていきます。
\begin{aligned} \dfrac{1}{2} &= \dfrac{Z - Z_1}{Z + Z_1} \\ Z &= 3Z_1 \\ \end{aligned}
ここで、\(Z\)はC点よりB側を見たインピーダンスなので、
\begin{aligned} Z &= R_1 + \dfrac{R_2 Z_2}{ R_2 + Z_2}\\ \end{aligned}
であり、これを代入すると
\begin{aligned} R_1 + \dfrac{R_2 Z_2}{ R_2 + Z_2} &= 3Z_1 \\ R_1 &= 3Z_1 - \dfrac{R_2 Z_2}{ R_2 + Z_2} \\ \end{aligned}
となりますので、答えは(ヨ)の\(\displaystyle 3Z_1-\frac{R_2Z_2}{R_2+Z_2}\)です。
なお、今まで求めた\(E + E_1 = R_1 i_3 + E_2\)、\(i_3 = \dfrac{ 2E }{ Z_1 + Z } \)、\(E_2 = \dfrac{ 2 \left( Z - R_1\right)}{ Z_1 + Z } E \)を用いても解けます。本来はこっちの方が正しいかと思います。
\begin{aligned} E + E_1 &= R_1 i_3 + E_2 \\ E + \dfrac{1}{2}E &= \dfrac{ 2E }{ Z_1 + Z } R_1 + \dfrac{ 2 \left( Z - R_1\right)}{ Z_1 + Z } E \\ \dfrac{3}{2}E &= \dfrac{ 2Z }{ Z_1 + Z } \\ 3Z_1 + 3Z &= 4Z \\ Z &= 3Z_1 \end{aligned}
以降の計算は同じです。
理論は時間がないので、電圧反射係数等を理解しておき、本番で計算を減らせるところは減らした方が合格に繋がりやすいかと思います。
- (1)ハ \(R_1i_3+E_2\)
- (2)ト \(\displaystyle \frac{R_2}{R_2+Z_2}\)
- (3)ヘ \(\displaystyle \frac{Z_1-Z}{Z_1+Z}i\)
- (4)ヲ \(\displaystyle \frac{2(Z-R_1)}{Z_1+Z}E\)
- (5)ヨ \(\displaystyle 3Z_1-\frac{R_2Z_2}{R_2+Z_2}\)