電験一種 H27年 理論 問5
次の文章は, 三相交流回路に関する記述である。文中の(0) に当てはまる最も適切なものを解答群の中から選べ。ただし, \(a\) は複素数で \(a = e^{j\frac{2}{3}\pi}\) とする。
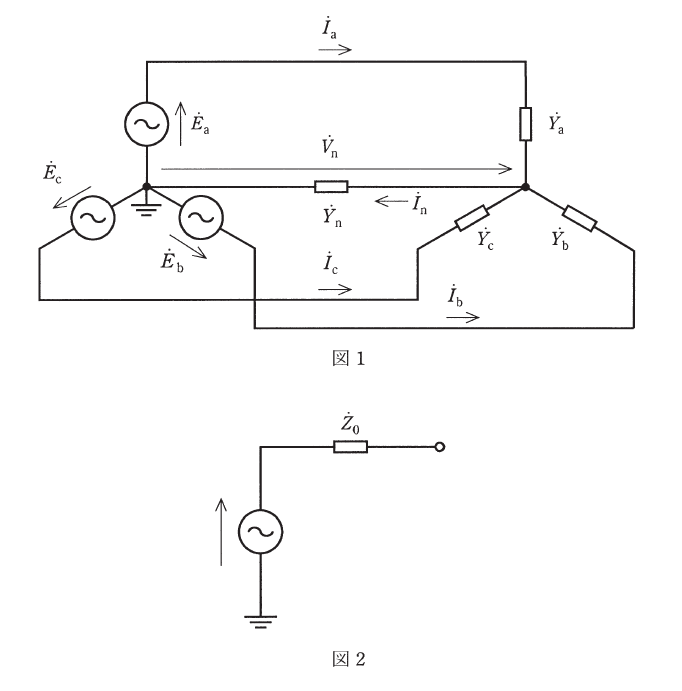
図1に示すように, 対称三相交流電源にアドミタンスが \(\dot{Y}_a, \dot{Y}_b, \dot{Y}_c\) の \(Y\) 形不平衡負荷を接続した。負荷と電源の中性点を結ぶ中性線のアドミタンスを \(\dot{Y}_n\) とする。\(\dot{E}_a = 100 \angle 0^\circ \text{ V}\)であり, 相回転は \(\dot{E}_a\), \(\dot{E}_b\), \(\dot{E}_c\) の順 (\(\dot{E}_b = a^2 \dot{E}_a\), \(\dot{E}_c = a \dot{E}_a\)) とする。\(Y\) 形不平衡負荷のアドミタンス \(\dot{Y}_a\), \(\dot{Y}_b\), \(\dot{Y}_c\) は以下の形とする。
\(\begin{pmatrix} \dot{Y}_a \\ \dot{Y}_b \\ \dot{Y}_c \end{pmatrix} = \begin{pmatrix} \dot{Y}_0 + \Delta \dot{Y} \\ \dot{Y}_0 + a \Delta \dot{Y} \\ \dot{Y}_0 + a^2 \Delta \dot{Y} \end{pmatrix}, \Delta \dot{Y} \ne 0 \cdots \text{①}\)
ここで, \(1+a+a^2 = 0\), \(a^3 = 1\) に注意する。
ミルマンの定理と①式を使うと, \(Y\) 形負荷の中性点電位 \(\dot{V}_n\) と中性線電流 \(\dot{I}_n\) の式は
\(\dot{V}_n = \) (1) \( , \dot{I}_n = \) (1) \(\times \dot{Y}_n \cdots \text{②}\)
となる。
図1の三相回路の中性点間を短絡又は開放したところ, 以下の結果を得た。
(a) 中性点間を短絡すると (\(\dot{Y}_n = \infty\)), 中性線電流は \(\dot{I}_n = 30a \text{ [A]}\) となった。
(b) 中性点間を開放すると (\(\dot{Y}_n = 0\)), \(Y\) 形負荷の中性点電位は \(\dot{V}_n = 100a \text{ [V]}\) となった。
②式に(a)と(b)の結果を適用すると, \((\dot{Y}_0, \Delta \dot{Y}) = \) (2) \([\text{S}]\) となる。
図1の回路を \(\dot{Y}_n\) から見た等価回路を図2のように表すと, (a)及び(b)から\(\dot{Z}_0 = \) (3) \(\Omega\) となる。したがって, 図1の回路の中性線で消費する電力が最大となるのは \(\dot{Y}_n = \) (4) \(\text{S}\) のときである。そのとき, 中性線で消費する電力は (5) \(\text{W}\) である。
| (イ) | \(300\) | (ロ) | \(\displaystyle \frac{10a}{3}\) | (ハ) | \(\displaystyle \frac{3a}{10}\) | (ニ) | \(\displaystyle \frac{3E_a \Delta \dot{Y}}{\dot{Y_0}+3\dot{Y_n}}\) |
| (ホ)(2) | \(\displaystyle \left(\frac{1}{10}, \frac{a}{10}\right)\) | (ヘ) | \(250\) | (ト) | \(\displaystyle \left(\frac{1}{10}, \frac{1}{10}\right)\) | (チ) | \(\displaystyle \left(\frac{1}{10}, \frac{a^2}{10}\right)\) |
| (リ)(3) | \(\displaystyle \frac{10}{3}\) | (ヌ)(5) | \(750\) | (ル) | \(\displaystyle \frac{3a^2}{10}\) | (ヲ)(1) | \(\displaystyle \frac{3\dot{E_a}\Delta \dot{Y}}{3\dot{Y_0}+\dot{Y_n}}\) |
| (ワ)(4) | \(\displaystyle \frac{3}{10}\) | (カ) | \(\displaystyle \frac{10a^2}{3}\) | (ヨ) | \(\displaystyle \frac{3\dot{E_a} \dot{Y}_n}{3\dot{Y_0}+\Delta\dot{Y}}\) |
出典:平成27年度第一種電気主任技術者理論科目B問題問5
解説
理屈が分かっていれば難しい問題ではないのでこのような問題で点数を稼ぎたいところです。
\(Y\)型負荷の中性点電位\(\dot{V_n}\)
問題ではミルマンの定理を使って答えを求めることとなっていますが、本番でミルマンの定理を思い出せなかった時のためにあえて別の解き方で解きます。ミルマンの定理が分かるのであればそれで解くのが一番早いです。それで解く場合は他参考書に解説があると思いますのでそれを参照してください。
キルヒホッフの第2法則に従い式を立てます。
\begin{aligned} \dot{E_a} &= \dfrac{\dot{I_a}}{\dot{Y_a}} + \dfrac{\dot{I_n}}{\dot{Y_n}} \\ \dot{E_b} &= \dfrac{\dot{I_b}}{\dot{Y_b}} + \dfrac{\dot{I_n}}{\dot{Y_n}} \\ \dot{E_c} &= \dfrac{\dot{I_c}}{\dot{Y_c}} + \dfrac{\dot{I_n}}{\dot{Y_n}} \\ \end{aligned}
これより\(\dot{V_n}\)を求めます。3つの式を足します。
\begin{aligned} \dot{E_a} + \dot{E_b} + \dot{E_c}&= \dfrac{\dot{I_a}}{\dot{Y_a}} + \dfrac{\dot{I_b}}{\dot{Y_b}} + \dfrac{\dot{I_c}}{\dot{Y_c}} + \dfrac{3\dot{I_n}}{\dot{Y_n}} \\ \end{aligned}
対称三相交流電圧源なので\(\dot{E_a} + \dot{E_b} + \dot{E_c} = 0\)です。
\begin{aligned} 0 &= \dfrac{\dot{I_a}}{\dot{Y_a}} + \dfrac{\dot{I_b}}{\dot{Y_b}} + \dfrac{\dot{I_c}}{\dot{Y_c}} + \dfrac{3\dot{I_n}}{\dot{Y_n}} \\ \end{aligned}
各電流を\(\dot{I_a} = \left( \dot{E_a} - \dot{V_n} \right) \dot{Y_a} \)の考え方を用いて消去します。
\begin{aligned} 0 &= \dot{E_a} - \dot{V_n} + \dot{E_b} - \dot{V_n} + \dot{E_c} - \dot{V_n} + \dfrac{3\left\{ \left( \dot{E_a} - \dot{V_n} \right) \dot{Y_a} + \left( \dot{E_b} - \dot{V_n} \right) \dot{Y_b} + \left( \dot{E_c} - \dot{V_n} \right) \dot{Y_c}\right\}}{\dot{Y_n}} \\ \dot{V_n} &= \dfrac{ \left( \dot{E_a} - \dot{V_n} \right) \dot{Y_a} + \left( \dot{E_b} - \dot{V_n} \right) \dot{Y_b} + \left( \dot{E_c} - \dot{V_n} \right) \dot{Y_c}}{\dot{Y_n}} \\ \dot{Y_n} \dot{V_n} &= \left( \dot{E_a} - \dot{V_n} \right) \dot{Y_a} + \left( \dot{E_b} - \dot{V_n} \right) \dot{Y_b} + \left( \dot{E_c} - \dot{V_n} \right) \dot{Y_c} \\ \dot{V_n} \left( \dot{Y_a} + \dot{Y_b} + \dot{Y_c} + \dot{Y_n} \right) &= \dot{E_a} \dot{Y_a} + \dot{E_b} \dot{Y_b} + \dot{E_c} \dot{Y_c} \end{aligned}
よって\(\dot{V_n}\)は以下となります。ミルマンの定理を覚えていればこれがすぐにでてきます。
\begin{aligned} \dot{V_n} &= \dfrac{ \dot{E_a} \dot{Y_a} + \dot{E_b} \dot{Y_b} + \dot{E_c} \dot{Y_c} } { \dot{Y_a} + \dot{Y_b} + \dot{Y_c} + \dot{Y_n} } \\ \end{aligned}
問題で与えられた条件を用いて整理します。
\begin{aligned} \dot{V_n} &= \dfrac{ \dot{E_a} \left( \dot{Y_0} + \Delta \dot{Y} \right) + a^2 \dot{E_a} \left( \dot{Y_0} + a \Delta \dot{Y} \right) + a \dot{E_a} \left( \dot{Y_0} + a^2 \Delta \dot{Y} \right) } { \left( \dot{Y_0} + \Delta \dot{Y} \right) + \left( \dot{Y_0} + a \Delta \dot{Y} \right) + \left( \dot{Y_0} + a^2 \Delta \dot{Y} \right) + \dot{Y_n} } \\ &= \dfrac{\dot{E}_a \dot{Y}_0(1+a+a^2)+3\dot{E}_a\Delta\dot{Y}}{3\dot{Y}_0+\Delta\dot{Y}(1+a+a^2)+\dot{Y}_n} \\ &= \dfrac{ 3 \dot{E_a} \Delta \dot{Y} } { 3\dot{Y_0} + \dot{Y_n} } \\ \end{aligned}
となり、答えは(ヲ)の\(\displaystyle \frac{3\dot{E_a}\Delta \dot{Y}}{3\dot{Y_0}+\dot{Y_n}}\)です。
(a)と(b)の結果を適用した時の\(\left( \dot{Y_0} ,\Delta \dot{Y} \right) \)
②式を用いて計算します。
(a)
\begin{aligned} \dot{I_n} &= \dfrac{3\dot{E_a}\Delta \dot{Y}}{3\dot{Y_0}+\dot{Y}_n} \times \dot{Y_n} \\ 30a &= \lim_{\dot{Y}_n \to \infty} \left( \frac{3\dot{E}_a \Delta\dot{Y}}{3\dot{Y}_0 + \dot{Y}_n} \times \dot{Y}_n \right) \\ &= \lim_{\dot{Y}_n \to \infty} \left( \dfrac{3\dot{E}_a \Delta\dot{Y}}{\dfrac{3\dot{Y}_0}{\dot{Y}_n} + 1} \right) \\ &= \frac{3\dot{E}_a \Delta\dot{Y}}{0 + 1} \\ &= 3\dot{E}_a \Delta\dot{Y} \\ 30a &= 300 \Delta\dot{Y} \\ \Delta\dot{Y} &= \dfrac{a}{10}\\ \end{aligned}
(b)
\begin{aligned} \dot{V_n} &= \frac{3\dot{E_a}\Delta \dot{Y}}{3\dot{Y_0}+\dot{Y_n}} \\ 100a &= \lim_{\dot{Y}_n \to 0} \left( \frac{3\dot{E_a}\Delta \dot{Y}}{3\dot{Y_0}+\dot{Y_n}} \right) \\ &= \frac{3\dot{E_a}\Delta \dot{Y}}{3\dot{Y_0}} \\ 100a &= \frac{300 \cdot \dfrac{a}{10}}{3\dot{Y_0}} \\ \dot{Y_0} &= \dfrac{1}{10} \\ \end{aligned}
よって答えは(ホ)の\(\displaystyle \left(\frac{1}{10}, \frac{a}{10}\right)\)です。
\(\dot{Y_n}\)から見た等価回路の時の\(\dot{Z_0}\)
\(\dot{Y_n}\)から見た等価回路の\(\dot{Z_0}\)は\(\dfrac{1}{\dot{Y_a}}\)、\(\dfrac{1}{\dot{Y_b}}\)、\(\dfrac{1}{\dot{Y_c}}\)の並列接続の時の抵抗なので
\begin{aligned} \dot{Z_0} &= \dfrac{1}{\dot{Y_a}+ \dot{Y_b} + \dot{Y_c}} \\ &= \dfrac{1}{3 \dot{Y_0}} \\ &= \dfrac{10}{3} \end{aligned}
よって答えは(リ)の\(\displaystyle \frac{10}{3}\)です。
中性線で消費する電力が最大となる\(\dot{Y_n}\)
消費電力最大の時、\(\dot{Y_n}\)は\(\dfrac{1}{\dot{Z_0}}\)の複素共役になるので
\begin{aligned} \dot{Y_n} &= \dfrac{1}{\overline{\dot{Z_0}}} \\ &= \dfrac{3}{10} \\ \end{aligned}
よって答えは(ワ)の\(\displaystyle \frac{3}{10}\)です。
\(\dot{Y_n}\)が複素共役になることについての補足
まず、複素電流\( \dot{I_n} \)の式から、アドミタンス\( \dot{Y_n} \)にかかる複素電圧\( \dot{V_{Yn}} \)を求めます。
\begin{aligned} \dot{I_n} &= \frac{\dot{V_n}}{\dot{Z_0} + \dfrac{1}{\dot{Y_n}}} = \frac{\dot{V_n} \dot{Y_n}}{\dot{Z_0}\dot{Y_n} + 1} \\ \end{aligned}
負荷アドミタンス\( \dot{Y_n} \)にかかる電圧\( \dot{V_{Yn}} \)は、\( \dot{I_n} \)と\( \dfrac{1}{\dot{Y_n}} \)の積なので、
\begin{aligned} \dot{V_{Yn}} &= \dot{I_n} \cdot \frac{1}{\dot{Y_n}} = \left(\frac{\dot{V_n} \dot{Y_n}}{\dot{Z_0}\dot{Y_n} + 1}\right) \cdot \frac{1}{\dot{Y_n}} = \frac{\dot{V_n}}{\dot{Z_0}\dot{Y_n} + 1} \\ \end{aligned}
次に、アドミタンス\( \dot{Y_n} \)で消費される電力\( P_n \)を計算します。交流回路の消費電力は、複素電力\( S_n = \dot{V_{Yn}} \overline{\dot{I_n}} \)の実部なので
\begin{aligned} P_n = \operatorname{Re}\left[ \dot{V_{Yn}} \overline{\dot{I_n}} \right] \\ \end{aligned}
ここで、\( \overline {\dot{I_n} } = \dfrac{\overline {\dot{V_n} } \overline { \dot{Y_n}}}{\overline{ \dot{Z_0}} \overline{ \dot{Y_n} } + 1} \)なので、
\begin{aligned} P_n &= \operatorname{Re}\left[ \frac{\dot{V_n}}{\dot{Z_0}\dot{Y_n} + 1} \cdot \dfrac{\overline {\dot{V_n} } \overline { \dot{Y_n}}}{\overline{ \dot{Z_0}} \overline{ \dot{Y_n} } + 1} \right] \\ & = \operatorname{Re}\left[ \frac{|\dot{V_n}|^2 \overline {\dot{Y_n} }}{(\dot{Z_0}\dot{Y_n} + 1)(\overline{ \dot{Z_0}} \overline{ \dot{Y_n} } + 1)} \right] \\ \end{aligned}
分母を展開すると、
\begin{aligned} (\dot{Z_0}\dot{Y_n} + 1)(\overline{ \dot{Z_0}} \overline{ \dot{Y_n} } + 1) &= |\dot{Z_0}|^2|\dot{Y_n}|^2 + 2\operatorname{Re} \left [ \dot{Z_0}\dot{Y_n} \right] + 1 \\ \end{aligned}
となり、\(P_n\)は以下で表されます。
\begin{aligned} P_n &= \frac{|\dot{V_n}|^2 \operatorname{Re}\left [ \dot{Y_n} \right] }{|\dot{Z_0}|^2|\dot{Y_n}|^2 + 2\operatorname{Re}\left[ \dot{Z_0}\dot{Y_n} \right] + 1} \\ \end{aligned}
\( P_n \)を最大にするには、分母を最小にする必要があります。\( \dot{Y_n} = G_n + jB_n \)、\( \dot{Z_0} = R_0 + jX_0 \)と表し、これらを\( P_n \)の式に代入します。
\begin{aligned} P_n &= \frac{|\dot{V_n}|^2 G_n}{(R_0^2+X_0^2)(G_n^2+B_n^2) + 2(R_0G_n - X_0B_n) + 1} \\ \end{aligned}
まず、\( P_n \)を\( B_n \)に関して最大化するため、分母を\( D_n \)として、\( \dfrac{\partial D_n}{\partial B_n} = 0 \)と置きます。
\begin{aligned} 0 &= \frac{\partial}{\partial B_n} \left\{ (R_0^2+X_0^2)(G_n^2+B_n^2) + 2R_0G_n - 2X_0B_n + 1 \right\} \\ 0 &= 2(R_0^2+X_0^2)B_n - 2X_0 \\ B_n &= \frac{X_0}{R_0^2+X_0^2} = \frac{X_0}{|\dot{Z_0}|^2} \end{aligned}
次に、\( P_n \)を\( G_n \)に関して最大化するため、\( \dfrac{D_n}{G_n} \)が最小になる条件を求めます。
\begin{aligned} \frac{D_n}{G_n} &= \dfrac{1}{G_n} \left\{ |\dot{Z_0}|^2 \left(G_n^2 + B_n^2 \right) + 2R_0 G_n - 2X_0 B_n + \frac{R_0^2 + X_0^2 }{|\dot{Z_0}|^2 } \right\} \\ &=\dfrac{1}{G_n} \left\{ |\dot{Z_0}|^2 G_n^2 + \dfrac{X_0^2 }{|\dot{Z_0}|^2} + 2R_0 G_n - \dfrac{2X_0^2 }{|\dot{Z_0}|^2} + \frac{R_0^2 + X_0^2 }{|\dot{Z_0}|^2 } \right\} \\ &= |\dot{Z_0}|^2 G_n + 2R_0 + \frac{R_0^2}{|\dot{Z_0}|^2 G_n} \\ \end{aligned}
この式を\(G_n \)に関して微分して0と置きます。
\begin{aligned} 0 &= \frac{d}{dG_n}\left(|\dot{Z_0}|^2 G_n + \frac{R_0^2}{|\dot{Z_0}|^2 G_n}\right) \\ &= |\dot{Z_0}|^2 - \frac{R_0^2}{|\dot{Z_0}|^2 G_n^2} \\ G_n &= \frac{R_0}{|\dot{Z_0}|^2} \\ \end{aligned}
以上の結果から、消費電力が最大となる条件は、
\begin{aligned} \dot{Y_n} &= G_n + jB_n = \frac{R_0}{|\dot{Z_0}|^2} + j\frac{X_0}{|\dot{Z_0}|^2} = \frac{R_0 + jX_0}{|\dot{Z_0}|^2} \\ \end{aligned}
となります。ここで、\( \dfrac{R_0 + jX_0}{|\dot{Z_0}|^2} = \dfrac{\dot{Z_0}}{|\dot{Z_0}|^2} = \dfrac{\dot{Z_0}}{\dot{Z_0} \overline {\dot{Z_0} } } = \dfrac{1}{\overline { \dot{Z_0}}} \) です。
よって、アドミタンス\( \dot{Y_n} \)での消費電力が最大になる条件は、\( \dot{Y_n} = \dfrac{1}{\overline {\dot{Z_0}}} \)です。
中性線で消費する電力
今まで求めた数値を用い計算します。
\begin{aligned} P &= |\dot{I_n} |^2 \operatorname{Re} \left [ \dfrac{1}{\dot{Y_n}} \right] \\ &= \left | \frac{\dot{V_n}}{\dot{Z_0} + \dfrac{1}{\dot{Y_n}}} \right | ^2 \operatorname{Re} \left [ \dfrac{1}{\dot{Y_n}} \right] \\ &= \left | \frac{100a }{\dfrac{10}{3}+\dfrac{10}{3}} \right | ^2 \times \dfrac{10}{3} \\ &= 225 \times \dfrac{10}{3} \\ &= 750 \end{aligned}
よって答えは(ヌ)の\(750\)です。
- (1)ヲ \(\displaystyle \frac{3\dot{E_a}\Delta \dot{Y}}{3\dot{Y_0}+\dot{Y_n}}\)
- (2)ホ \(\displaystyle \left(\frac{1}{10}, \frac{a}{10}\right)\)
- (3)リ \(\displaystyle \frac{10}{3}\)
- (4)ワ \(\displaystyle \frac{3}{10}\)
- (5)ヌ \(750\)