電験一種 H27年 理論 問3
次の文章は, 直流回路に関する記述である。文中の(0) に当てはまる最も適切なものを解答群の中から選びなさい。
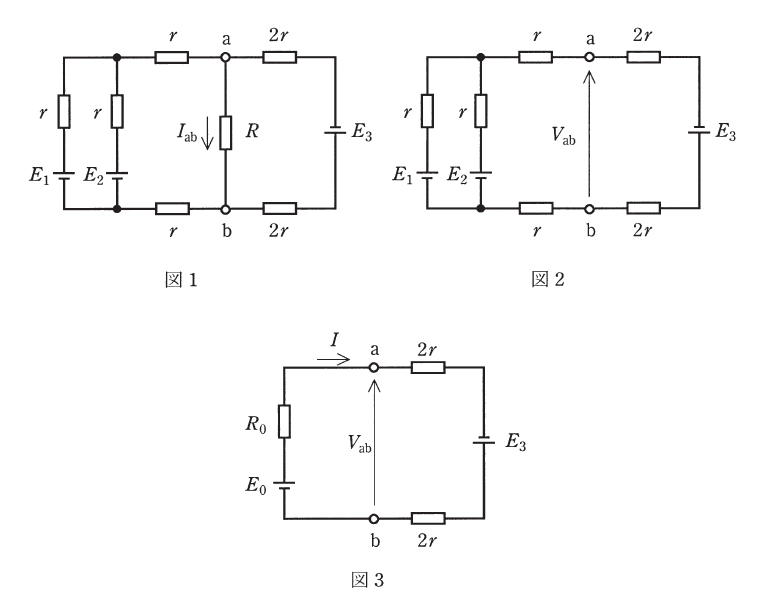
図1に示す回路において, 抵抗 \(R\) に流れる電流 \(I_{ab}\) をテブナンの定理を用いて求めたい。
まず, 抵抗 \(R\) を取り除いた図2の回路は, 端子 \(a\)-\(b\)間から左側部分を整理すると図3のように表される。図3の電圧 \(E_0\) は \(E_0 = \) (1), 抵抗 \(R_0\) は \(R_0 = \dfrac{5}{2}r\) となる。
図3に示すように電流 \(I\) をとれば \(I = \) (2) となるから, 端子 \(a\)-\(b\)間に現れる電圧 \(V_{ab}\) (端子 \(b\) を基準とする) は \(V_{ab} = \) (3) となる。
次に, 図3の直流電源を短絡除去した場合において, 端子 \(a\)-\(b\)間から回路をみた抵抗 \(R_{ab}\) は, \(R_{ab} = \) (4) となるから, (3) 及び (4) より, 抵抗 \(R\) に流れる電流 \(I_{ab}\) は, \(I_{ab} = \) (5) となる。
| (イ) | \(\displaystyle \frac{E_1-E_2}{2}\) | (ロ) | \(\displaystyle \frac{2(E_1+E_2)-E_3}{13R+21r}\) | (ハ) | \(2r\) |
| (ニ) | \(\displaystyle \frac{2(E_1+E_2)-E_3}{13}\) | (ホ)(5) | \(\displaystyle \frac{4(E_1+E_2)-5E_3}{13R+20r}\) | (ヘ) | \(E_1+E_2\) |
| (ト) | \(\displaystyle \frac{21}{13}r\) | (チ)(2) | \(\displaystyle \frac{E_1+E_2+2E_3}{13r}\) | (リ) | \(\displaystyle \frac{E_1+E_2-2E_3}{4}\) |
| (ヌ) | \(\displaystyle \frac{E_1+E_2+2E_3}{16r}\) | (ル)(1) | \(\displaystyle \frac{E_1+E_2}{2}\) | (ヲ)(4) | \(\displaystyle \frac{20}{13}r\) |
| (ワ) | \(\displaystyle \frac{E_1+E_2-2E_3}{4R+8r}\) | (カ) | \(\displaystyle \frac{2(E_1+E_2+E_3)}{13r}\) | (ヨ)(3) | \(\displaystyle \frac{4(E_1+E_2)-5E_3}{13}\) |
出典:平成27年度第一種電気主任技術者理論科目A問題問3
解説
難しいことは問われていないので冷静に正答したい問題です。
図3の電圧\(E_0\)
図2の\(V_{ab}\)の左側を見て開放電圧を求めます。
\(V_{ab}\)の右側を開放するとそちらには電流は流れないので、\(E_1\)と\(E_2\)による電圧だけ考えれば問題ありません。
\(E_1\)による\(E_2\)の方にある\(r\)の電圧降下は図より\(\dfrac{E_1-E_2}{2}\)です。
開放電圧はこれと\(E_2\)の和ですから、
\begin{aligned} \dfrac{E_1-E_2}{2} + E_2 &= \dfrac{E_1+E_2}{2} \end{aligned}
となり、答えは(ル)の\(\displaystyle \frac{E_1+E_2}{2}\)です。
なお、\(E_2\)側から考えても同様の結果が得られます。
図3の電流\(I\)
\(E_0\)、\(R_0\)が分かっていますのでそのまま計算します。
\begin{aligned} I &= \dfrac{E_0 + E_3}{R_0 + 2r + 2r} \\ &= \dfrac{\dfrac{E_1 + E_2}{2} + E_3}{\dfrac{5}{2}r + 4r} \\ &= \dfrac{E_1 + E_2 + 2E_3}{13r } \\ \end{aligned}
よって答えは(チ)の\(\displaystyle \frac{E_1+E_2+2E_3}{13r}\)です。
端子bを基準とした電圧\(V_{ab}\)
\begin{aligned} V_{ab} &= 2rI - E_3 + 2rI \\ &= 4rI - E_3 \\ &= 4r \cdot \dfrac{E_1 + E_2 + 2E_3}{13r } - E_3 \\ &= \dfrac{4\left( E_1 + E_2 \right) + 8E_3}{13} - \dfrac{13}{13}E_3 \\ &= \dfrac{4\left( E_1 + E_2 \right) + 8E_3}{13} - \dfrac{13}{13}E_3 \\ &= \dfrac{4\left( E_1 + E_2 \right) - 5E_3}{13} \\ \end{aligned}
よって答えは(ヨ)の\(\displaystyle \frac{4(E_1+E_2)-5E_3}{13}\)です。
端子a-b間から回路を見た抵抗\(R_{ab}\)
端子a-b間から回路を見ると\(R_0\)と\(2r+2r\)の並列接続となりますので、
\begin{aligned} R_{ab} &= \dfrac{4rR_0}{R_0+4r} \\ &= \dfrac{4r \cdot \dfrac{5}{2}r }{ \dfrac{5}{2}r+4r} \\ &= \dfrac{20}{13}r \\ \end{aligned}
となり、答えは(ヲ)の\(\displaystyle \frac{20}{13}r\)です。
Rに流れる電流\(I_{ab}\)
テブナンの定理にのっとり計算します。
\begin{aligned} I_{ab} &= \dfrac{V_{ab}}{R_{ab}+ R } \\ &= \dfrac{\dfrac{4(E_1+E_2)-5E_3}{13}}{\dfrac{20}{13}r+R} \\ &= \dfrac{4(E_1+E_2)-5E_3}{20r+13R} \\ &= \dfrac{4(E_1+E_2)-5E_3}{13R+20r} \\ \end{aligned}
よって答えは(ホ)の\(\displaystyle \frac{4(E_1+E_2)-5E_3}{13R+20r}\)です。
- (1)ル \(\displaystyle \frac{E_1+E_2}{2}\)
- (2)チ \(\displaystyle \frac{E_1+E_2+2E_3}{13r}\)
- (3)ヨ \(\displaystyle \frac{4(E_1+E_2)-5E_3}{13}\)
- (4)ヲ \(\displaystyle \frac{20}{13}r\)
- (5)ホ \(\displaystyle \frac{4(E_1+E_2)-5E_3}{13R+20r}\)