電験一種 H27年 理論 問2
次の文章は, 直流遮断器の開放機構などに応用される電磁石に関する磁気回路に関する記述である。文中の(0) に当てはまる最も適切なものを解答群の中から選びなさい。
図1に固定された鉄心Bに鉄心Aが吸着されている電磁石を示している。鉄心Bには巻線1及び巻線2が巻かれており, 直流電流\(I_1\)及び\(I_2\)で励磁されている。鉄心Aにはばねの力が図の左方向に作用しており, 電磁石の吸着力がばねのけん引力よりも弱まると, 鉄心Aが鉄心Bから離れる仕組みとなっている。
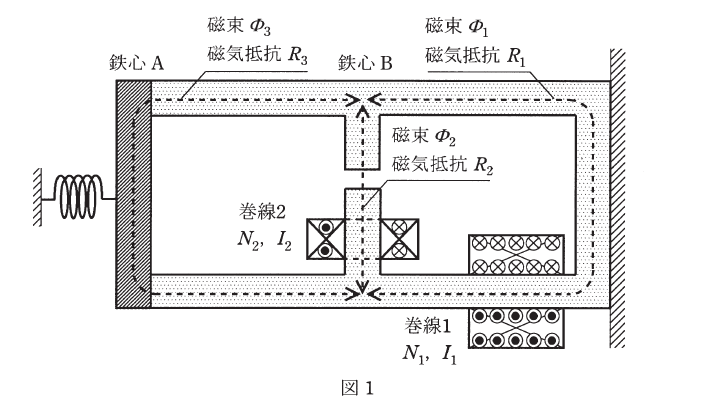
図1の電磁石を磁気回路で示したのが図2である。磁気抵抗\(R_1\)は, 鉄心Bの右側部分の磁気抵抗で, 断面積\(S\), 長さ\(L\)とすると\(R_1 = \) (1) と表される。磁気抵抗\(R_2\)は, 鉄心Bの中央部分の磁気抵抗で, 断面積\(S\), 長さ\(l\)(空隙部分を含む), 空隙部分の長さを\(g\)(\(g \ll l\))とすると\(R_2 = \) (2) と表される。このとき, 鉄心A, Bの比透磁率を\(\mu_r\), 空気の透磁率を\(\mu_0\)とする。
鉄心Bの左側と鉄心Aからなる部分の磁路の磁気抵抗を\(R_3\)とし, 図2で示すように各部の磁束を\(\Phi_1, \Phi_2, \Phi_3\)とするとき, 以下の磁気回路の方程式が得られる。
\(\Phi_1 = \Phi_2 + \Phi_3 \cdots \text{①}\)
\(N_1 I_1 = \) (3) \(\cdots \text{②}\)
\(N_1 I_1 + N_2 I_2 = R_1 \Phi_1 + R_2 \Phi_2 \cdots \text{③}\)
このとき, ①式~③式を用いて磁束 \(\Phi_3\) を求めると, 磁気抵抗 \(R_1, R_2, R_3\) 及び \(N_1, N_2, I_1, I_2\) を用いて磁束 \(\Phi_3\) は次式で表され, 主回路電流 \(I_2\) が増すと磁束 \(\Phi_3\) が減少することが分かる。
\(\Phi_3 = \) (4)
磁気抵抗 \(R_1, R_2, R_3\) をそれぞれ, \(R_1 = R_3 = 2.0 \times 10^5 \text{ A}/\text{Wb}\), \(R_2 = 1.0 \times 10^7 \text{ A}/\text{Wb}\), 巻線 1 の巻数を \(N_1 = 500\), 電流を \(I_1 = 0.9 \text{ A}\), 巻線 2 の巻数を \(N_2 = 2\) とする。また, 鉄心Aの部分の磁束 \(\Phi_3\) が \(0.5 \text{ mWb}\) まで減少したとき, 鉄心Aが鉄心Bから離れることとする。このとき, 巻線2を流れる主回路電流\(I_2\)が (5) \(\text{kA}\) に達したときに直流遮断器を自動的に開放させる機構として, この電磁石を利用することができる。
| (イ) | \(\displaystyle \frac{R_1N_1I_1-R_2N_2I_2}{R_1R_2+R_2R_3+R_3R_1}\) | (ロ) | \(R_1\Phi_1+R_2\Phi_2\) | (ハ)(1) | \(\displaystyle \frac{L}{\mu_r\mu_0S}\) |
| (ニ) | \(\displaystyle \frac{\mu_r\mu_0S}{L}\) | (ホ) | \(\displaystyle \frac{R_1R_2+R_2R_3+R_3R_1}{R_2N_2I_2-R_1N_1I_1}\) | (ヘ) | \(0.23\) |
| (ト) | \(\displaystyle \frac{\mu_r\mu_0(l-g)}{S}+\frac{\mu_0g}{S}\) | (チ)(4) | \(\displaystyle \frac{R_2N_1I_1-R_1N_2I_2}{R_1R_2+R_2R_3+R_3R_1}\) | (リ) | \(\displaystyle \frac{\mu_r\mu_0L}{S}\) |
| (ヌ)(2) | \(\displaystyle \frac{l-g}{\mu_r\mu_0S}+\frac{g}{\mu_0S}\) | (ル)(3) | \(R_1\Phi_1+R_3\Phi_3\) | (ヲ)(5) | \(6.2\) |
| (ワ) | \(\displaystyle \frac{g(l-g)}{\mu_0S(l-g)+\mu_r\mu_0Sg}\) | (カ) | \(1.5\) | (ヨ) | \(R_2\Phi_2+R_3\Phi_3\) |
出典:平成27年度第一種電気主任技術者理論科目A問題問2
解説
磁気回路の問題は多くはないですが、難しいことは問われていないため冷静に解きたいところです。
磁気抵抗\(R_1\)
基本的な問題です。磁気抵抗は長さが長いほど大きくなり、断面積が大きいほど小さくなります。また、透磁率が大きいほど小さくなります。
抵抗からイメージできる内容をあてはめればそのまま答えになります。
答えは(ハ)の\(\displaystyle \frac{L}{\mu_r\mu_0S}\)です。
磁気抵抗\(R_2\)
(1)と同様の考えでOKですが空隙部分を含むためそれを考慮する必要があります。
空隙部分は長さ\(g\)、それ以外の部分の長さは\(l-g\)であり、全体としての磁気抵抗はこれらの直列接続になりますので
\begin{aligned} R_2 &= \frac{l-g}{\mu_r\mu_0S}+\frac{g}{\mu_0S} \\ \end{aligned}
となり、答えは(ヌ)の\(\displaystyle \frac{l-g}{\mu_r\mu_0S}+\frac{g}{\mu_0S}\)です。
磁気回路の方程式\(N_1 I_1\)
外側を周る磁気回路を考えたとき、起磁力は\(N_1 I_1\)、そこの磁束と磁気抵抗は\(R_1 \Phi_1 \)、\(R_3 \Phi_3 \)ですから
\begin{aligned} N_1 I_1 &= R_1\Phi_1+R_3\Phi_3 \\ \end{aligned}
となりますので、答えは(ル)の\(R_1\Phi_1+R_3\Phi_3\)です。
磁束\(\Phi_3\)
①~③の式を利用して磁束\(\Phi_3\)を求めます。
\begin{cases} \Phi_1 = \Phi_2 + \Phi_3 \quad & (1) \\ N_1I_1 = R_1\Phi_1 + R_3\Phi_3 \quad & (2) \\ N_1I_1 + N_2I_2 = R_1\Phi_1 + R_2\Phi_2 \quad & (3) \end{cases}
\(\Phi_2\) を消去します。
\begin{align*} N_1I_1 + N_2I_2 &= R_1\Phi_1 + R_2(\Phi_1 - \Phi_3) \\ N_1I_1 + N_2I_2 &= R_1\Phi_1 + R_2\Phi_1 - R_2\Phi_3 \\ (N_1I_1 + N_2I_2) &= (R_1 + R_2)\Phi_1 - R_2\Phi_3 \quad (4) \end{align*}
\(\Phi_1\) を消去します。
(2)式と(4)式から \(\Phi_1\) を消去します。(2)式を \(\Phi_1\) について解きます。
\begin{align*} R_1\Phi_1 &= N_1I_1 - R_3\Phi_3 \\ \Phi_1 &= \frac{N_1I_1 - R_3\Phi_3}{R_1} \quad (5) \end{align*}
(5)式を(4)式に代入します。
\begin{aligned} N_1I_1 + N_2I_2 &= (R_1 + R_2)\left(\frac{N_1I_1 - R_3\Phi_3}{R_1}\right) - R_2\Phi_3 \\ R_1(N_1I_1 + N_2I_2) &= (R_1 + R_2)(N_1I_1 - R_3\Phi_3) - R_1R_2\Phi_3 \\ \end{aligned}
式を展開して整理します。
\begin{align*} R_1N_1I_1 + R_1N_2I_2 &= R_1N_1I_1 - R_1R_3\Phi_3 + R_2N_1I_1 - R_2R_3\Phi_3 - R_1R_2\Phi_3 \\ R_1N_2I_2 - R_2N_1I_1 &= (-R_1R_3 - R_2R_3 - R_1R_2)\Phi_3 \\ R_2N_1I_1 - R_1N_2I_2 &= (R_1R_2 + R_2R_3 + R_3R_1)\Phi_3 \end{align*}
最後に \(\Phi_3\) について解きます。
\begin{aligned} \Phi_3 = \frac{R_2N_1I_1 - R_1N_2I_2}{R_1R_2 + R_2R_3 + R_3R_1} \\ \end{aligned}
よって答えは(チ)の\(\displaystyle \frac{R_2N_1I_1-R_1N_2I_2}{R_1R_2+R_2R_3+R_3R_1}\)です。
主回路電流\(I_2\)
数値を代入して\(I_2\)を求めます。
\begin{aligned} \Phi_3 &= \frac{R_2N_1I_1 - R_1N_2I_2}{R_1R_2 + R_2R_3 + R_3R_1} \\ 0.5 \times 10^{-3} &= \frac{1.0 \times 10^7 \times 500 \times 0.9 - 2.0 \times 10^5 \times 2 \times I_2}{2.0 \times 10^5 \times 1.0 \times 10^7 + 1.0 \times 10^7 \times 2.0 \times 10^5 + 2.0 \times 10^5 \times 1.0 \times 10^5} \\ 0.5 \times 10^{-3} &= \frac{45000 \times 10^5 - 4I_2 \times 10^5}{404 \times 10^{10}} \\ 0.5 \times 10^{-3} \times 404 \times 10^{5} &= 45000 - 4I_2 \\ 20200 &= 45000 - 4I_2 \\ 4I_2 &= 24800 \\ I_2 &= 6200 \\ \end{aligned}
解答は[kA]とすることを求められているので答えは(ヲ)の\(6.2\)です。
- (1)ハ \(\displaystyle \frac{L}{\mu_r\mu_0S}\)
- (2)ヌ \(\displaystyle \frac{l-g}{\mu_r\mu_0S}+\frac{g}{\mu_0S}\)
- (3)ル \(R_1\Phi_1+R_3\Phi_3\)
- (4)チ \(\displaystyle \frac{R_2N_1I_1-R_1N_2I_2}{R_1R_2+R_2R_3+R_3R_1}\)
- (5)ヲ \(6.2\)