電験一種 H27年 理論 問1
次の文章は, 誘電体中の静電界の基本性質に関する記述である。文中の(0) に当てはまる最も適切なものを解答群の中から選べ。
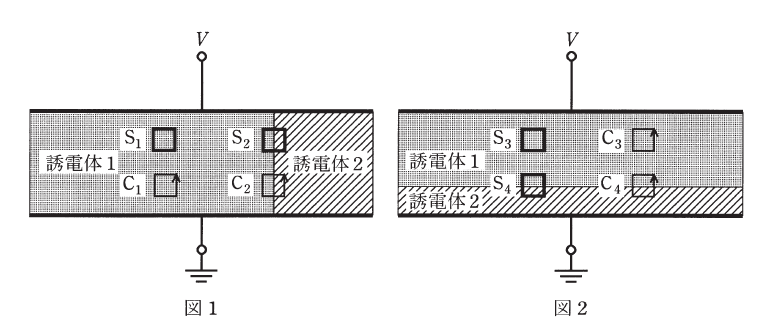
長方形の導体平板を極板とする平行平板コンデンサが二つある。このコンデンサに, 異なる誘電率をもつ2種類の直方体の誘電体を, 隙間のないよう, かつ極板からはみ出さないように挿入する。一つは図1のように, 二つの誘電体の境界面が極板と垂直になっており, もう一つは図2のように, 二つの誘電体の境界面が極板と平行になっている。共に, 極板間には電位差 \(V \left( \ne 0 \right) \) が与えられている。ただし, 図1及び図2は横から見た図であり, 端効果はないものとする。
これに対し, 図1及び図2に示したように, 紙面と平行に置かれた長方形の閉周積分路 \(C_1 \sim C_4\) と, 紙面と平行な面及び極板と平行な面をもつように置かれた直方体の閉曲面 \(S_1 \sim S_4\) を仮定する。\(\text{C}_1 \sim \text{C}_4\), \(\text{S}_1 \sim \text{S}_4\)は全て誘電体内に存在し, \(\text{C}_2\), \(\text{C}_4\), \(\text{S}_2\), \(\text{S}_4\)は二つの誘電体の境界面を横切っているものとする。
コンデンサ内の電界 \(\boldsymbol{E} \), 電束密度 \(\boldsymbol{D}\) と分極 \(\boldsymbol{P}\) を考える。これらの関係式は, 真空中の誘電率を \(\varepsilon_0\)とすると, (1) となる。また, 空間内の電界のエネルギー密度は, (2) で表される。
次に, \(\boldsymbol{E} \), \(\boldsymbol{D}\), \(\boldsymbol{P}\) を長方形 \(C_1 \sim C_4\) でそれぞれ閉周積分することを考える。このとき, \(C_1 \sim C_4\)のうちの(3) については, \(\boldsymbol{D}\) と \(\boldsymbol{P}\) の閉周積分は零にならない。
今度は, \(\boldsymbol{E} \), \(\boldsymbol{D}\), \(\boldsymbol{P}\) を直方体 \(S_1 \sim S_4\) でそれぞれ面積分することを考える。このとき, \(S_1 \sim S_4\)のうちの(4) については, \(\boldsymbol{E} \), \(\boldsymbol{D}\), \(\boldsymbol{P}\)のうちの(5) の面積分は零にならない。
| (イ) | \(\boldsymbol{E}\)と\(\boldsymbol{D}\) | (ロ) | \(\boldsymbol{P} = \varepsilon_0 \boldsymbol{E}+\boldsymbol{D}\) | (ハ) | \(S_1\)と\(S_3\) | (ニ) | \(S_2\) |
| (ホ)(1) | \(\boldsymbol{D} = \varepsilon_0 \boldsymbol{E}+\boldsymbol{P}\) | (ヘ)(4) | \(S_4\) | (ト) | \(C_1\)と\(C_3\) | (チ) | \(\boldsymbol{D}\) |
| (リ) | \(C_4\) | (ヌ) | \(\displaystyle \frac{1}{2}\boldsymbol{E}^2\) | (ル)(3) | \(C_2\) | (ヲ) | \(\boldsymbol{D} = \varepsilon_0 (\boldsymbol{E}+\boldsymbol{P})\) |
| (ワ)(2) | \(\displaystyle \frac{1}{2}\boldsymbol{E} \cdot \boldsymbol{D}\) | (カ)(5) | \(\boldsymbol{E}\)と\(\boldsymbol{P}\) | (ヨ) | \(\displaystyle \frac{1}{2}\boldsymbol{E} \times \boldsymbol{D}\) |
出典:平成27年度第一種電気主任技術者理論科目A問題問1
解説
電磁気学をしっかり学んでいなければある程度割り切って暗記で対応する問題かと思います。
ちゃんと理解する場合は専門書を読む必要があります。
参考になるYoutubeの動画(自分は製作者ではありません)
コンデンサ内の電界 \(\boldsymbol{E} \), 電束密度 \(\boldsymbol{D}\) と分極 \(\boldsymbol{P}\) の関係
真空コンデンサの場合は\(\boldsymbol{D} = \varepsilon_0 \boldsymbol{E}\)とよくみる関係となります。
今回のように誘電体で満たされている場合、分極\(\boldsymbol{P}\)が発生し、
\(\boldsymbol{D} = \varepsilon_0 \boldsymbol{E}+\boldsymbol{P}\)
となります。
答えは(ホ)の\(\boldsymbol{D} = \varepsilon_0 \boldsymbol{E}+\boldsymbol{P}\)です。
空間内の電界のエネルギー密度
結論としては答えは(ワ)の\(\displaystyle \frac{1}{2}\boldsymbol{E} \cdot \boldsymbol{D}\)です。
これについてはコンデンサのエネルギー、\(\dfrac{1}{2} CV^2\)から考えるのが楽かと思います。
\begin{aligned} \dfrac{1}{2} CV^2 &= \dfrac{1}{2} \cdot \dfrac{\varepsilon_0 S}{d} \left(Ed\right)^2 \\ &= \dfrac{1}{2} \varepsilon_0 E^2 Sd \\ \end{aligned}
ここで、\(Sd\)は誘電体の体積になるためエネルギー密度は
\begin{aligned} \dfrac{1}{2} \varepsilon_0 E^2 &= \dfrac{1}{2} ED \\ \end{aligned}
となります。なお、(ヨ)の\(\displaystyle \frac{1}{2}\boldsymbol{E} \times \boldsymbol{D}\)は、\(\boldsymbol{E}\)と\(\boldsymbol{D}\)の直行成分を考えると感覚的におかしいため選択肢からは外せます。
厳密な理解はさておき、問題を解くだけであればこれで正答はできるかと思います。
\(\boldsymbol{D}\)と\(\boldsymbol{P}\)の周回積分が零にならない\(C\)
図1においては、間隔を\(d\)とした時誘電体1でも誘電体2でも電界は\(\dfrac{V}{d}\)で同じです。
電界は同じですが誘電率が異なるため、電束密度は異なります。
\(\boldsymbol{D} = \varepsilon_0 \boldsymbol{E}+\boldsymbol{P}\)の式から考えると、この時\(\boldsymbol{D}\)と\(\boldsymbol{P}\)は誘電体1と2では異なることが分かります。
また、図2においては電束密度が連続なため誘電体1と2では電束密度は等しいです。
誘電率が異なることからそれぞれで電界\(\boldsymbol{E}\)は異なります。
\(\boldsymbol{D} = \varepsilon_0 \boldsymbol{E}+\boldsymbol{P}\)の式から考えると、電界\(\boldsymbol{E}\)がそれぞれ異なりますが電束密度\(\boldsymbol{D}\)が等しくならないといけないため、こちらでも\(\boldsymbol{P}\)は異なるということになります。
まとめると、それぞれの誘電体において
図1
\(\boldsymbol{D}\)と\(\boldsymbol{P}\)が異なる
図2
\(\boldsymbol{E}\)と\(\boldsymbol{P}\)が異なる
ということになります。
この前提に基づき、周回積分した時に\(\boldsymbol{D}\)と\(\boldsymbol{P}\)が零にならない長方形\(C\)を考えます。
まず、同じ誘電体の中は極板と平行な区間の線積分は零で、垂直な区間は経路の向きが逆で零になるためこれは零になります。
よって\(C_2\)と\(C_4\)について考えます。
\(C_2\)
上で考えた通り、図1では\(\boldsymbol{D}\)と\(\boldsymbol{P}\)は誘電体1と2では異なります。
よって周回積分した時に左右では\(\boldsymbol{D}\)と\(\boldsymbol{P}\)が異なることになり、打ち消し合い零になることがありません。
よってこれは周回積分した時に\(\boldsymbol{D}\)と\(\boldsymbol{P}\)が零になりません。
\(C_4\)
上で考えた通り、図2では\(\boldsymbol{E}\)と\(\boldsymbol{P}\)が誘電体1と2では異なります。
ただし、周回積分の際は左右で同じだけ誘電体1と2を含むため、結局これらは打ち消し合い零となります。
よって、周回積分した時に\(\boldsymbol{D}\)と\(\boldsymbol{P}\)が零にならないのは\(C_2\)だけであり、答えは(ル)です。
面積分した時零にならない\(S\)
ここでも(3)と同様に同じ誘電体の中の面積分は考える必要がないので\(S_2\)と\(S_4\)についてのみ考えます。
\(S_2\)
上で考えた通り、図1では\(\boldsymbol{D}\)と\(\boldsymbol{P}\)は誘電体1と2では異なります。
しかし、極板に平行な面において、上の面と下の面で各誘電体の大きさは同じなので、ここは打ち消し合い零になります。
上から入る\(\boldsymbol{E}\)、\(\boldsymbol{D}\)、\(\boldsymbol{P}\)と下から出てくる\(\boldsymbol{E}\)、\(\boldsymbol{D}\)、\(\boldsymbol{P}\)は同じだということです。
\(S_4\)
上で考えた通り、図2では\(\boldsymbol{E}\)と\(\boldsymbol{P}\)が誘電体1と2では異なります。
\(S_2\)と同様に考えると、こちらでは上から入る\(\boldsymbol{E}\)、\(\boldsymbol{P}\)と下から出てくる\(\boldsymbol{E}\)、\(\boldsymbol{P}\)の大きさは違います。
よって\(\boldsymbol{E}\)と\(\boldsymbol{P}\)の面積分は零になりません。
なお、\(\boldsymbol{D}\)は連続なので面積分は零になります。
したがって、\(S_4\)では面積分は零にならないため答えは(ヘ)です。
\(\boldsymbol{E}\)、\(\boldsymbol{D}\)、\(\boldsymbol{P}\)のうちどの面積分が零にならないか
ここまで考えてきた通り、\(S_4\)では\(\boldsymbol{E}\)と\(\boldsymbol{P}\)の面積分は零になりません。
よって答えは(カ)の\(\boldsymbol{E}\)と\(\boldsymbol{P}\)です。
- (1)ホ \(\boldsymbol{D} = \varepsilon_0 \boldsymbol{E}+\boldsymbol{P}\)
- (2)ワ \(\displaystyle \frac{1}{2}\boldsymbol{E} \cdot \boldsymbol{D}\)
- (3)ル \(C_2\)
- (4)ヘ \(S_4\)
- (5)カ \(\boldsymbol{E}\)と\(\boldsymbol{P}\)