電験一種 H26年 理論 問6
次の文章は,MIS構造においてのしきい値に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選びなさい。なお,\(\varepsilon_0\)は真空の誘電率,\(\varepsilon_s\)は半導体の比誘電率,\(\varepsilon_{ox}\)は絶縁体の比誘電率とする。
金属-絶縁物-p形半導体からなるMIS構造において,電圧を印加しないときに半導体内のバンドが一直線であるフラットバンド状態になっているとする。そこからゲートに正方向に電圧をを加えると,正孔は半導体表面近傍から存在しなくなり空乏層になる。このときp形半導体のキャリア濃度を\(N_A\),空乏層の厚さを\(l_D\)とすると,空乏層内の厚さ方向\(x\)における電位\(\phi\)の勾配は,絶縁物-半導体界面を\(x=0\)として
\(\dfrac{\mathrm{d}\phi}{\mathrm{d}x}=\dfrac{qN_A}{\varepsilon_s\varepsilon_0}(x-l_D)\)
で与えられる。\(x=l_D\)において電位が零として式を解くと\(\phi(x)=\) (1)と表され,\(x=0\)での電位(表面電位)は\(\phi_s=\) (2)となる。ここで,空乏状態となった領域でのアクセプタによる単位面積当たりの電荷は\(Q=-qN_Al_D\)であり,この電荷が絶縁物内に電位差を作る。絶縁物層厚を\(t_{ox}\)とすると,この電位差は (3)である。 (2)と (3)の和がゲート電圧である。
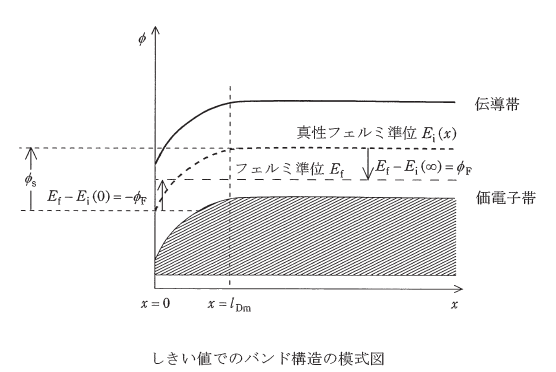
ゲートに印加される電圧が大きくなると,表面電位\(\phi_s\)も大きくなる。図右側に示す様にp形半導体の平衡状態(\(x=\infty\))においてフェルミ準位\(E_f\)と真性フェルミ準位\(E_i(\infty)\)の差の電位がフェルミポテンシャル\(\phi_f\)であるが,表面電位\(\phi_s\)が\(2\phi_f\)となった図のようなバンド構造のときに,電子の濃度は半導体表面の濃度\(N_A\)と等しくなる。このときのゲート電圧をしきい値と呼ぶ。しきい値よりもゲート電圧が大きくなっても,それに伴い増える電荷は半導体表面の電荷のみであり,空乏層の厚さは変化しない。このしきい値で最大になる空乏層厚さ\(l_{Dm}\)は (4)である。しきい値は,表面電位にしきい層\(l_{Dm}\)の空乏層の電荷が絶縁層に作る電位差を足したものとなり, (5)となる。
| (イ)(3) | \(\displaystyle \frac{Qt_{ox}}{\varepsilon_{ox}\varepsilon_0}\) | (ロ) | \(\displaystyle \sqrt{\frac{\phi_{F}\varepsilon_{ox}\varepsilon_0}{qN_A}}\) | (ハ)(1) | \(\displaystyle \frac{qN_A}{2\varepsilon_s\varepsilon_0}(x-l_D)^2\) |
| (ニ) | \(\displaystyle \frac{qN_A}{\varepsilon_s\varepsilon_0}x^2\) | (ホ)(5) | \(\displaystyle 2\phi_{F}+\frac{qN_Al_{Dm}t_{ox}}{\varepsilon_{ox}\varepsilon_0}\) | (ヘ) | \(\displaystyle \frac{qN_A}{2\varepsilon_s\varepsilon_0}l_D\) |
| (ト) | \(\displaystyle \frac{qN_A}{\varepsilon_s\varepsilon_0}{l_D}^2\) | (チ)(2) | \(\displaystyle \frac{qN_A}{2\varepsilon_s\varepsilon_0}{l_D}^2\) | (リ) | \(\displaystyle \frac{Q\varepsilon_{ox}\varepsilon_0}{t_{ox}}\) |
| (ヌ) | \(\displaystyle 2\phi_F+\frac{qN_Al_{Dm}t_{ox}}{2\varepsilon_{ox}\varepsilon_0}\) | (ル) | \(\displaystyle \frac{qN_A}{2\varepsilon_s\varepsilon_0}(x-l_D)\) | (ヲ) | \(\displaystyle \sqrt{\frac{4\phi_{F}\varepsilon_{ox}\varepsilon_0}{qN_A}}\) |
| (ワ) | \(\displaystyle \frac{Qt_{ox}}{2\varepsilon_{ox}\varepsilon_0}\) | (カ) | \(\displaystyle 2\phi_F+\frac{qN_Al_{Dm}\varepsilon_{ox}\varepsilon_0}{t_{ox}}\) | (ヨ)(4) | \(\displaystyle \sqrt{\frac{4\phi_{F}\varepsilon_s\varepsilon_0}{qN_A}}\) |
出典:平成26年度第一種電気主任技術者理論科目B問題問6
解説
この手の問題は電験では読解である程度拾えるようにはなっているので、焦らず冷静に問題を読み込むことが重要です。
このサイト全般においてそうですが、学術的な話は専門書を読んでください。ここは試験合格を目的としているので、問題を解くことを優先しており、理論的な話はあまりありません。
\(x=l_D\)において電位が零として式を解いた時の\(\phi(x)\)
問題の微分方程式を解きます。
\begin{aligned} \frac{\mathrm{d}\phi}{\mathrm{d}x} &= \frac{qN_A}{\varepsilon_s\varepsilon_0}(x-l_D) \\ \int d\phi &= \int \frac{qN_A}{\varepsilon_s\varepsilon_0}(x-l_D)dx \\ \phi(x) &= \frac{qN_A}{\varepsilon_s\varepsilon_0} \left( \frac{1}{2}x^2 - l_D x \right) + C \quad \text{(Cは積分定数)}\\ \end{aligned}
問題に書かれた初期条件 \(x=l_D\) で \(\phi(l_D)=0\) を用いて、定数 \(C\) を決定します。
\begin{aligned} \phi(l_D) &= \frac{qN_A}{\varepsilon_s\varepsilon_0} \left( \frac{1}{2}l_D^2 - l_D \cdot l_D \right) + C = 0 \\ C &= -\frac{qN_A}{\varepsilon_s\varepsilon_0} \left( -\frac{1}{2}l_D^2 \right) = \frac{qN_A}{2\varepsilon_s\varepsilon_0} l_D^2 \end{aligned}
定数 \(C\) を代入して答えを求めます。
\begin{aligned} \phi(x) &= \frac{qN_A}{\varepsilon_s\varepsilon_0} \left( \frac{1}{2}x^2 - l_D x \right) + \frac{qN_A}{2\varepsilon_s\varepsilon_0} l_D^2 \\ &= \frac{qN_A}{2\varepsilon_s\varepsilon_0} (x^2 - 2l_D x + l_D^2) \\ &= \frac{qN_A}{2\varepsilon_s\varepsilon_0} (x - l_D)^2 \\ \end{aligned}
よって答えは(ハ)の\(\displaystyle \frac{qN_A}{2\varepsilon_s\varepsilon_0}(x-l_D)^2\)です。
\(x=0\)での電位(表面電位)\(\phi_s\)
(1)の答えに\(x=0\)を代入します。
\begin{aligned} \phi_s &= \frac{qN_A}{2\varepsilon_s\varepsilon_0}(0-l_D)^2 \\ &= \frac{qN_A}{2\varepsilon_s\varepsilon_0}{l_D}^2 \\ \end{aligned}
よって答えは(チ)の\(\displaystyle \frac{qN_A}{2\varepsilon_s\varepsilon_0}{l_D}^2\)です。
絶縁物内の電位差
平行平板コンデンサの電界は\(E=\dfrac{Q}{\varepsilon_0 S}\)で表されます。
これと同じ考え方で、問題に与えられている電荷\(Q\)は単位面積あたりであること、比誘電率を考慮すると電界\(E\)は
\begin{aligned} E &= \dfrac{Q}{\varepsilon_{ox} \varepsilon_0} \\ \end{aligned}
問題で求められているのは電位差ですから、ここに絶縁物の厚さをかけます。
\begin{aligned} V &= E t_{ox} \\ &= \dfrac{Qt_{ox}}{\varepsilon_{ox} \varepsilon_0} \\ \end{aligned}
よって答えは(イ)の\(\displaystyle \frac{Qt_{ox}}{\varepsilon_{ox}\varepsilon_0}\)です。
この問題は(イ)、(リ)、(ワ)が解答の候補になりますが、(リ)の単位が違うことが分かれば後は分母に2がつくかつかないかだけの問題となります。
ここで平行平板コンデンサの電界を思い出せれば問題の意味が分からなくても答えを選べると思います。
空乏層厚さ\(l_{Dm}\)
問題を読み込むと、表面電位\(\phi_s\)が\(2\phi_F\)の時のゲート電圧がしきい値で、この時の空乏層厚さを問われていることが分かります。
表面電位は(2)で求めたので、それを用いて空乏層厚さを求めます。
\begin{aligned} \phi_s &= \frac{qN_A}{2\varepsilon_s\varepsilon_0}{l_D}^2 \\ 2\phi_F &= \frac{qN_A}{2\varepsilon_s\varepsilon_0}{l_{Dm}}^2 \\ {l_{Dm}}^2 &= \frac{4\phi_F\varepsilon_s\varepsilon_0}{qN_A} \\ l_{Dm} &= \sqrt{\dfrac{4\phi_F\varepsilon_s\varepsilon_0}{qN_A}} \\ \end{aligned}
よって答えは(ヨ)の\(\displaystyle \sqrt{\frac{4\phi_{F}\varepsilon_s\varepsilon_0}{qN_A}}\)です。
しきい値
問題に書いてある通り、表面電位に厚さ\(l_{Dm}\)の空乏層の電荷が絶縁層に作る電位差を足します。
問題の電荷が負(\(Q= -qN_A l_D\))なので符号が関係しますが、そもそも選択肢にないためこの問題においては悩む必要はありません。
(3)の答えに\(Q= -qN_A l_{Dm}\)、を代入したものと、しきい値の時の表面電位\(2\phi_F\)を足します。
\begin{aligned} 2\phi_{F}+\frac{qN_Al_{Dm}t_{ox}}{\varepsilon_{ox}\varepsilon_0} \\ \end{aligned}
よって答えは(ホ)の\(\displaystyle 2\phi_{F}+\frac{qN_Al_{Dm}t_{ox}}{\varepsilon_{ox}\varepsilon_0}\)です。
(5)は(3)が分かれば消去法で解ける問題かと思います。そういう意味では書いてあることは難しいですが問題を解くだけであれば難しくはありません。ただ、本番では問6なのもあり時間の猶予がないためそう簡単ではないと思います。
この問題をしっかり理解することも大事ですが、過去問をとにかく周回し、時間を掛けずに解ける問題を増やして読解に割ける時間を増やすというのも試験においては重要かと思います。
- (1)ハ \(\displaystyle \frac{qN_A}{2\varepsilon_s\varepsilon_0}(x-l_D)^2\)
- (2)チ \(\displaystyle \frac{qN_A}{2\varepsilon_s\varepsilon_0}{l_D}^2\)
- (3)イ \(\displaystyle \frac{Qt_{ox}}{\varepsilon_{ox}\varepsilon_0}\)
- (4)ヨ \(\displaystyle \sqrt{\frac{4\phi_{F}\varepsilon_s\varepsilon_0}{qN_A}}\)
- (5)ホ \(\displaystyle 2\phi_{F}+\frac{qN_Al_{Dm}t_{ox}}{\varepsilon_{ox}\varepsilon_0}\)