電験一種 H26年 理論 問5
次の文章は,三相交流回路に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選びなさい。ただし,\(a\)は複素数で \(a=e^{j\frac{2}{3}\pi}\) とする。
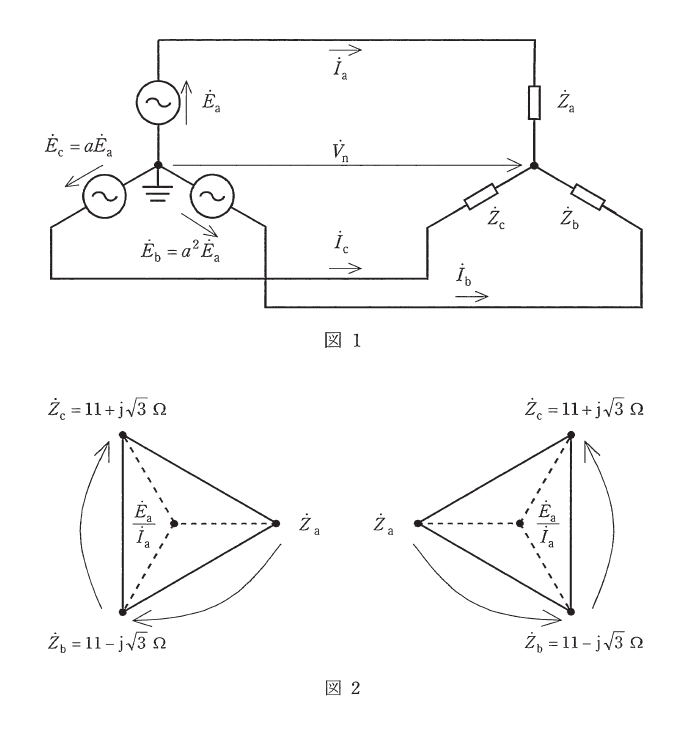
図1のように対称三相交流電圧源に\(Y\)形不平衡負荷を接続した。
\( \dot{E}_a=120 V \angle 0^\circ\)であり,相回転は\(\dot{E}_a, \dot{E}_b, \dot{E}_c\)の順とする。この相回転の順を式で表すと
\( \dot{E}_b=a^2\dot{E}_a, \dot{E}_c=a\dot{E}_a\) …①
となる。いま,回路の線電流 \(\dot{I}_a, \dot{I}_b, \dot{I}_c\) も対称三相であり,
\( \dot{I}_b=a^2\dot{I}_a, \dot{I}_c=a\dot{I}_a\) …②
の関係式を満たしているものとする。このとき,\(Y\)形不平衡負荷の各相の電圧平衡の式は
\( \dot{I}_a \dot{Z}_a = \dot{E}_a - \) (1),\( \dot{I}_b \dot{Z}_b = \dot{E}_b - \) (1),\( \dot{I}_c \dot{Z}_c = \dot{E}_c - \) (1) …③
であるから,①式と②式を利用すると,③式より\(Y\)形不平衡負荷のインピーダンスは
\begin{aligned} \begin{pmatrix} \dot{Z}_a \\ \dot{Z}_b \\ \dot{Z}_c \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \frac{\dot{E}_a}{\dot{I}_a} - \boxed{\vphantom{2}\hspace{1em} \text{(2)} \vphantom{2} \hspace{1em}} \frac{\dot{V}_n}{\dot{I}_a} \quad \cdots \text{④} \\ \end{aligned}
と表すことができる。ただし,\(a^3=1\)に注意する。
ここで,①式と②式が成立して,\(\dot{Z}_b=11-j\sqrt{3}\Omega\),\(\dot{Z}_c=11+j\sqrt{3}\Omega\)であるときを考える。④式に従って\(\dot{Z}_a, \dot{Z}_b, \dot{Z}_c\)を複素平面上にプロットすると,これらは中心が\(\dfrac{\dot{E}_a}{\dot{I}_a}\)である正三角形の頂点をなし,図2のどちらかになる。なお,\(\dot{Z}_a\)と\(\dfrac{\dot{E}_a}{\dot{I}_a}\)は実軸上に位置している。図2の二つの三角形のうち,④式と整合する正三角形を形成する\(\dot{Z}_a=\) (3) \(\Omega\),\(\dot{I}_a=\) (4) A,\(V_n=\) (5) Vであることが分かる。
| (イ) | \(a^2\dot{V}_n\) | (ロ) | 14 | (ハ) | 13 | (ニ) | 16 |
| (ホ)(3) | 8 | (ヘ)(5) | 24 | (ト)(1) | \(\dot{V}_n\) | (チ) | \(a\dot{V}_n\) |
| (リ) | 32 | (ヌ) | -20 | (ル)(4) | 12 | (ヲ) | 10 |
| (ワ)(2) | \(\begin{pmatrix}1\\a\\a^2\end{pmatrix}\) | (カ) | \(\begin{pmatrix}1\\a^2\\a\end{pmatrix}\) | (ヨ) | \(\begin{pmatrix}a\\a^2\\1\end{pmatrix}\) |
出典:平成26年度第一種電気主任技術者理論科目B問題問5
解説
図形が絡む問題はあまりないため本番で見ると焦るかもしれませんが、冷静に解ければ難しい問題ではありません。
\(Y\)形不平衡負荷の各相の電圧平衡の式
図1より、中性点の電圧は\(\dot{V}_n\)であることから、\( \dot{E}_a = \dot{I}_a \dot{Z}_a + \dot{V}_n \) となります。問題の式になるように移項すると
\begin{aligned} \dot{I}_a \dot{Z}_a &= \dot{E}_a - \dot{V}_n \\ \end{aligned}
となります。これは他の相でも同様です。よって答えは(ト)の\(\dot{V}_n\)です。
\(Y\)形不平衡負荷のインピーダンス
問題にある各式を整理します。ここで、\(a^3=1\)であることを使用します。
\begin{aligned} \dot{I}_a \dot{Z}_a &= \dot{E}_a - \dot{V}_n \\ \dot{Z}_a &= \dfrac{\dot{E}_a}{\dot{I}_a} - \dfrac{\dot{V}_n}{\dot{I}_a} \\ \end{aligned}
\begin{aligned} \dot{I}_b \dot{Z}_b &= \dot{E}_b - \dot{V}_n \\ \dot{Z}_b &= \dfrac{\dot{E}_b}{\dot{I}_b} - \dfrac{\dot{V}_n}{\dot{I}_b} \\ \dot{Z}_b &= \dfrac{a^2 \dot{E}_a}{a^2 \dot{I}_a} - \dfrac{a^3 \dot{V}_n}{a^2 \dot{I}_a} \\ \dot{Z}_b &= \dfrac{\dot{E}_a}{\dot{I}_a} - \dfrac{a \dot{V}_n}{ \dot{I}_a} \\ \end{aligned}
\begin{aligned} \dot{I}_c \dot{Z}_c &= \dot{E}_c - \dot{V}_n \\ \dot{Z}_c &= \dfrac{\dot{E}_c}{\dot{I}_c} - \dfrac{\dot{V}_n}{\dot{I}_c} \\ \dot{Z}_c &= \dfrac{a \dot{E}_a}{a \dot{I}_a} - \dfrac{a^3 \dot{V}_n}{a \dot{I}_a} \\ \dot{Z}_c &= \dfrac{\dot{E}_a}{\dot{I}_a} - \dfrac{a^2 \dot{V}_n}{ \dot{I}_a} \\ \end{aligned}
これらを行列式にします。
\begin{aligned} \begin{pmatrix} \dot{Z}_a \\ \dot{Z}_b \\ \dot{Z}_c \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \frac{\dot{E}_a}{\dot{I}_a} - \begin{pmatrix} 1 \\ a \\ a^2 \\ \end{pmatrix} \frac{\dot{V}_n}{\dot{I}_a} \end{aligned}
よって答えは(ワ)の\(\begin{pmatrix}1\\a\\a^2\end{pmatrix}\)です。
正三角形を利用して\(\dot{Z}_a\)を求める
まず、図としては図2の右の図形になります。
というのも、(2)で求めたインピーダンス、
\begin{aligned} \dot{Z}_a &= \dfrac{\dot{E}_a}{\dot{I}_a} - \dfrac{\dot{V}_n}{\dot{I}_a} \\ \end{aligned}
から考えると、は\(\dfrac{\dot{E}_a}{\dot{I}_a}\)は正の実数なので、図1の左が正しく\(\dot{Z}_a \gt \dfrac{\dot{E}_a}{\dot{I}_a}\)になる場合は\(\dfrac{\dot{V}_n}{\dot{I}_a}\)が負にならないといけません。
しかし、
\begin{aligned} \dot{Z}_b &= \dfrac{\dot{E}_a}{\dot{I}_a} - \dfrac{a \dot{V}_n}{ \dot{I}_a} \\ \dot{Z}_c &= \dfrac{\dot{E}_a}{\dot{I}_a} - \dfrac{a^2 \dot{V}_n}{ \dot{I}_a} \\ \end{aligned}
ここから\(\dfrac{ \dot{V}_n}{ \dot{I}_a}\)を求めると、
\begin{aligned} \dot{Z}_b - \dot{Z}_c &= \dfrac{\dot{E}_a}{\dot{I}_a} -\dfrac{\dot{E}_a}{\dot{I}_a} - \dfrac{a \dot{V}_n}{ \dot{I}_a} + \dfrac{a^2 \dot{V}_n}{ \dot{I}_a} \\ 11 - j\sqrt{3} - 11 - j\sqrt{3} &= \left(-a + a^2 \right)\dfrac{ \dot{V}_n}{ \dot{I}_a} \\ j2\sqrt{3} &= \left(a - a^2 \right)\dfrac{ \dot{V}_n}{ \dot{I}_a} \\ j2\sqrt{3} &= \left(-\dfrac{1}{2} + j\dfrac{\sqrt{3}}{2} + \dfrac{1}{2} + j\dfrac{\sqrt{3}}{2} \right)\dfrac{ \dot{V}_n}{ \dot{I}_a} \\ j2\sqrt{3} &= j\sqrt{3} \dfrac{ \dot{V}_n}{ \dot{I}_a} \\ \dfrac{ \dot{V}_n}{ \dot{I}_a} &= 2 \\ \end{aligned}
となり、\(\dfrac{\dot{V}_n}{\dot{I}_a}\)は正であることが分かるので、図は右が正しいということになります。
後は、上式より\(\dfrac{\dot{E}_a}{\dot{I}_a}\)を求めるか、図形から計算します。下は図形の例です。
\(\dot{Z}_b\)、\(\dot{Z}_c\)から考えると正三角形の一辺の長さは\(2\sqrt{3}\)となります。
よって、\(\dot{Z}_a\)は
\begin{aligned} \dot{Z}_a &= 11 - 2\sqrt{3} \cos \dfrac{\pi}{6} \\ &= 11 - 3 \\ &= 8 \\ \end{aligned}
となります。
また、\(\dfrac{\dot{E}_a}{\dot{I}_a}\)は正三角形の中心にあたるため、2:1に内分されることから、
\begin{aligned} \dfrac{\dot{E}_a}{\dot{I}_a} &= 8 + \left(11-3\right) \times \dfrac{2}{3} \\ &= 10 \\ \end{aligned}
となります。
\(\dfrac{\dot{V}_n}{\dot{I}_a}\)は、上でも求めていますが
\begin{aligned} \dfrac{\dot{V}_n}{\dot{I}_a} &= \dfrac{\dot{E}_a}{\dot{I}_a} - \dot{Z}_a\\ &= 10 - 8 \\ &= 2 \\ \end{aligned}
となります。
これを\(\dot{Z}_b\)と\(\dot{Z}_c\)の式に代入して正しいか確かめます。
\begin{aligned} \dot{Z}_b &= \dfrac{\dot{E}_a}{\dot{I}_a} - \dfrac{a \dot{V}_n}{ \dot{I}_a} \\ &= 10 - 2a \\ &= 11 - j\sqrt{3} \\ \end{aligned}
\begin{aligned} \dot{Z}_c &= \dfrac{\dot{E}_a}{\dot{I}_a} - \dfrac{a^2 \dot{V}_n}{ \dot{I}_a} \\ &= 10 - 2a^2 \\ &= 11 + j\sqrt{3} \\ \end{aligned}
答えとして正しいことが分かりました。(3)は\(\dot{Z}_a\)を問われているので、答えは(ホ)の8です。
正三角形を利用して\(\dot{I}_a\)を求める
\(\dfrac{\dot{E}_a}{\dot{I}_a}\)が分かっていて、\(\dot{E}_a\)は問題で与えられていますので
\begin{aligned} \dot{I}_a &= \dfrac{\dot{E}_a}{10} \\ &= \dfrac{120}{10} \\ &= 12 \\ \end{aligned}
よって答えは(ル)の12です。
正三角形を利用して\(\dot{V}_n\)を求める
今まで求めた数値を用い計算します。
\begin{aligned} \dot{V}_n &= 2 \dot{I}_a \\ &= 2 \times 12 \\ &= 24 \\ \end{aligned}
よって答えは(ヘ)の24です。
- (1)ト \(\dot{V}_n\)
- (2)ワ \(\begin{pmatrix}1\\a\\a^2\end{pmatrix}\)
- (3)ホ 8
- (4)ル 12
- (5)ヘ 24