電験一種 H26年 理論 問4
次の文章は,回路の過渡現象に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選びなさい。
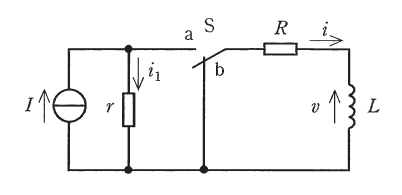
図のようにスイッチSと直流電流源\(I\),インダクタンス\(L\)のコイル,抵抗\(R\)及び\(r\)が接続されている。ただし\(r>R\)である。\(L\)に流れる電流\(i\)を,スイッチの動作が次の二つの場合においてそれぞれ求めたい。\(L\)の両端の電圧\(v\)を図のように定める。
a.時間\(t \lt 0\)では,スイッチSはa側であり,回路は定常状態である。\(t=0\)においてSをb側に切り替えた。
\(t>0\)における\(i\)の時間的変化について考える。このとき,\(R\)と\(L\)は閉路になっている。よって,
\(Ri+v=0\) …①
ここで,\(v=L\dfrac{\mathrm{d}i}{\mathrm{d}t}\)より
\(L\dfrac{\mathrm{d}i}{\mathrm{d}t}+Ri=0\) …②
\(t=0\)のとき\(i=\) (1)より,②式を解くと
\(i=\) (2)
b.時間\(t \lt 0\)では,スイッチSはb側であり,回路は定常状態である。\(t=0\)においてSをa側に切り替えた。\(r\)に流れる電流を\(i_1\)とする。
\(t>0\)において
\(\left. \begin{aligned} i_1 + i &= I \\ Ri + v &= \boxed{\vphantom{2}\hspace{1em} \text{(3)} \vphantom{2} \hspace{1em}} \end{aligned} \right\} \quad \cdots \text{③} \)
が成り立つ。\(t=0\)のときの\(i\)を考慮して\(t>0\)における\(i\)を求めると
\(i=\) (4)となる。
また,\(i=i_1\)となる時刻\(T\)は
\(T=\) (5)となる。
| (イ) | \(\displaystyle \frac{r}{R+r}Ie^{-\frac{R+r}{L}t}\) | (ロ)(2) | \(\displaystyle \frac{r}{r+R}Ie^{-\frac{R}{L}t}\) | (ハ) | \(\displaystyle \frac{R}{r+R}I\) |
| (ニ) | \(r(I-i_1)\) | (ホ)(5) | \(\displaystyle \frac{L}{R+r}\ln\frac{2r}{r-R}\) | (ヘ) | \(r(I+i_1)\) |
| (ト)(4) | \(\displaystyle \frac{r}{R+r}I\left(1-e^{-\frac{R+r}{L}t}\right)\) | (チ)(3) | \(ri_1\) | (リ)(1) | \(\displaystyle \frac{r}{r+R}I\) |
| (ヌ) | \(\displaystyle \frac{R}{r+R}Ie^{-\frac{R}{L}t}\) | (ル) | \(\displaystyle Ie^{-\frac{R}{L}t}\) | (ヲ) | \(\displaystyle \frac{2r}{R+r}I\left(1-e^{-\frac{R+r}{L}t}\right)\) |
| (ワ) | \(\displaystyle \frac{1}{(R+r)L}\ln\frac{2r}{r-R}\) | (カ) | \(I\) | (ヨ) | \(\displaystyle \frac{L}{r+R}\ln\frac{R+r}{r}\) |
出典:平成26年度第一種電気主任技術者理論科目A問題問4
解説
電圧源ではなく電流源であるところが珍しい問題ですが、難しいことは問われていないので得点源としたい問題です。
\(t=0\)のときの\(i\)
\(t=0\)の時電流は変化がないため抵抗による分流のみ考えます。
\begin{aligned} i &= \dfrac{r}{r+R} I \\ \end{aligned}
よって答えは(リ)の\(\displaystyle \frac{r}{r+R}I\)です。
②式を解いた結果の\(i\)
この問題の場合は時定数も気にする必要はありますが、慣れている人だと\(t=0\)の時\(\dfrac{r}{r+R} I\)で\(t = \infty\)の時\(0\)になる答えを選べばいいので計算は不要かもしれません。
答えは(ロ)の\(\displaystyle \frac{r}{r+R}Ie^{-\frac{R}{L}t}\)です。
以下計算の過程です。与えられた式は以下の通りです。
\begin{aligned} L\dfrac{\mathrm{d}i}{\mathrm{d}t} + Ri = 0 \\ \end{aligned}
変数分離します。
\begin{aligned} L\frac{di}{dt} &= -Ri \\ \frac{di}{i} &= -\frac{R}{L}dt \\ \end{aligned}
両辺を積分します。
\begin{aligned} \int \frac{1}{i}di = \int -\frac{R}{L}dt \\ \ln|i| = -\frac{R}{L}t + C_1 \end{aligned}
両辺を指数関数で表し、積分定数を整理します。
\begin{aligned} |i| &= e^{-\frac{R}{L}t + C_1} = e^{C_1}e^{-\frac{R}{L}t} \\ i(t) &= Ae^{-\frac{R}{L}t} \quad (\text{ただし、} A = \pm e^{C_1}) \\ \end{aligned}
初期値 \(i(0) = \dfrac{r}{r+R}I\) を用いて、定数 \(A\) を決定します。
\begin{aligned} i(0) &= Ae^{-\frac{R}{L}(0)} = A \\ A &= \frac{r}{r+R}I \\ \end{aligned}
したがって、微分方程式の解は以下のようになります。
\begin{aligned} i(t) = \frac{r}{r+R}I e^{-\frac{R}{L}t} \\ \end{aligned}
\(t \gt 0\)において成り立つ\(Ri + v\)
この場合並列回路になり各電圧降下は等しいので
\begin{aligned} Ri + v = ri_1 \\ \end{aligned}
が成り立ちます。
よって答えは(チ)の\(ri_1\)です。
\(t \gt 0\)のときの\(i\)
この問題も慣れている人だと\(t=0\)の時\(\ 0 \)で\(t = \infty\)の時\( \dfrac{r}{r+R}I\)になる答えを選べばいいので計算は不要かもしれません。
答えは(ト)の\(\displaystyle \frac{r}{R+r}I\left(1-e^{-\frac{R+r}{L}t}\right)\)です。
以下、微分方程式の解き方です。
\(i_1+i=I\)と\( v= L\dfrac{\mathrm{d}i}{\mathrm{d}t} \)を用いて式を整理します。
\begin{aligned} Ri + v &= ri_1 \\ Ri + L\dfrac{\mathrm{d}i}{\mathrm{d}t} &= r\left( I-i \right) \\ L\dfrac{\mathrm{d}i}{\mathrm{d}t} + \left( R + r \right)i &= rI \\ \end{aligned}
まず過渡解を求めます。 \(L\dfrac{\mathrm{d}i}{\mathrm{d}t} + (R+r)i = 0\) を解きます。この解を \(i_t\) とします。
\begin{aligned} L\frac{\mathrm{d}i_t}{\mathrm{d}t} = -(R+r)i_t \\ \frac{\mathrm{d}i_t}{i_t} = -\frac{R+r}{L}\mathrm{d}t \\ \end{aligned}
両辺を積分します。
\begin{aligned} \int \frac{1}{i_t}\mathrm{d}i_t &= \int -\frac{R+r}{L}\mathrm{d}t \\ \ln|i_t| &= -\frac{R+r}{L}t + C_1 \\ i_t(t) &= Ae^{-\frac{R+r}{L}t} \\ \end{aligned}
定常解 \(i_s\) を求めます。定常状態では電流は一定となり \(\frac{\mathrm{d}i}{\mathrm{d}t} = 0\) となるため、\(i_s\) は次の式から導かれます。
\begin{aligned} L(0) + (R+r)i_s &= rI \\ i_s &= \frac{rI}{R+r} \\ \end{aligned}
一般解 \(i(t)\) は、過渡解と定常解の和で表されます。
\begin{aligned} i(t) = i_t(t) + i_s = Ae^{-\frac{R+r}{L}t} + \frac{rI}{R+r} \\ \end{aligned}
初期条件 \(i(0) = 0\) を用いて、定数 \(A\) を決定します。
\begin{aligned} i(0) &= Ae^{-\frac{R+r}{L}(0)} + \frac{rI}{R+r} = 0 \\ A + \frac{rI}{R+r} &= 0 \\ A &= -\frac{rI}{R+r} \\ \end{aligned}
定数 \(A\) の値を一般解に代入して、最終的な解を得ます。
\begin{aligned} i(t) = -\frac{rI}{R+r}e^{-\frac{R+r}{L}t} + \frac{rI}{R+r} \\ i(t) = \frac{r}{R+r}I\left(1 - e^{-\frac{R+r}{L}t}\right) \\ \end{aligned}
\(i=i_1\)となる時刻\(T\)
\(i=i_1\)の時、\(i_1 + i = I\)なので
\begin{aligned} i_1 + i = I \\ i + i = I \\ i = \dfrac{I}{2} \\ \end{aligned}
となります。この時の\(t\)が\(T\)なので
\begin{aligned} i(t) = \frac{r}{R+r}I\left(1 - e^{-\frac{R+r}{L}t}\right) \\ \dfrac{I}{2} = \frac{r}{R+r}I\left(1 - e^{-\frac{R+r}{L}T}\right) \\ \dfrac{R+r}{2r} = 1 - e^{-\frac{R+r}{L}T} \\ e^{-\frac{R+r}{L}T} = \dfrac{r-R}{2r} \\ \end{aligned}
となります。ここからTを求めます。
\begin{aligned} \ln\left(e^{-\frac{R+r}{L}T}\right) &= \ln\left(\frac{r - R}{2r}\right) \\ -\frac{R+r}{L}T &= \ln\left(\frac{r - R}{2r}\right) \\ T &= -\frac{L}{R+r} \ln\left(\frac{r - R}{2r}\right) \\ T &= \frac{L}{R+r} \ln\left(\frac{2r}{r - R}\right) \\ \end{aligned}
よって答えは(ホ)の\(\displaystyle \frac{L}{R+r}\ln\frac{2r}{r-R}\)です。
- (1)リ \(\displaystyle \frac{r}{r+R}I\)
- (2)ロ \(\displaystyle \frac{r}{r+R}Ie^{-\frac{R}{L}t}\)
- (3)チ \(ri_1\)
- (4)ト \(\displaystyle \frac{r}{R+r}I\left(1-e^{-\frac{R+r}{L}t}\right)\)
- (5)ホ \(\displaystyle \frac{L}{R+r}\ln\frac{2r}{r-R}\)