電験一種 H26年 理論 問3
次の文章は,直流回路に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選びなさい。
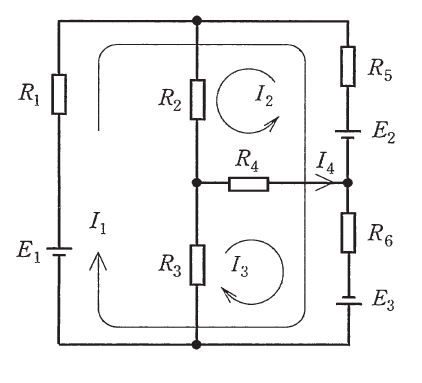
図に示す電圧源 \(E_1, E_2, E_3\) 及び抵抗 \(R_1, R_2, R_3, R_4, R_5, R_6\) を接続した回路において,網目電流(閉路電流) \(I_1, I_2, I_3\) を図のようにとると,これらに関する網目方程式は次式のように表される。

次に,\(R_1=R_2=R_3=R_4=R_5=R_6=R\) として,このときの電流 \(I_1\) 及び \(R_4\) に流れる電流 \(I_4\) を \(E_1, E_2, E_3\) 及び \(R\) を用いて表せば,\(I_1=\) (4),\(I_4=\) (5)となる。
| (イ)(3) | \(\displaystyle R_3+R_4+R_6\) | (ロ)(1) | \(R_1+R_5+R_6\) | (ハ) | \(\displaystyle \frac{E_2-E_3}{4R}\) | (ニ) | \(\displaystyle \frac{4E_1-E_2-E_3}{8R}\) |
| (ホ) | \(\displaystyle \frac{2E_1-E_2+E_3}{8R}\) | (ヘ) | \(R_1-R_5+R_6\) | (ト) | \(\displaystyle \frac{E_1-E_2+E_3}{4R}\) | (チ) | \(R_3+R_4\) |
| (リ) | \(-R_4\) | (ヌ) | \(-R_1+R_5+R_6\) | (ル)(4) | \(\displaystyle \frac{2E_1-E_2+E_3}{4R}\) | (ヲ)(2) | \(R_4\) |
| (ワ) | \(R_3-R_4+R_6\) | (カ)(5) | \(\displaystyle \frac{E_2+E_3}{4R}\) | (ヨ) | \(\displaystyle R_3+R_4-R_6\) |
出典:平成26年度第一種電気主任技術者理論科目A問題問3
解説
難しいことは問われていないのでしっかり解きたい問題です。
網目方程式(1)
外側のループについて考えます。
\begin{aligned} R_1I_1+R_5(I_1-I_2)+R_6(I_1+I_3)&=E_1-E_2+E_3 \\ (R_1+R_5+R_6)I_1-R_5I_2+R_6I_3&=E_1-E_2+E_3 \end{aligned}
よって答えは(ロ)の\(R_1+R_5+R_6\)です。
網目方程式(2)
同様に右上のループについて考えます。
\begin{aligned} R_5(I_2-I_1)+R_2I_2+R_4(I_2+I_3)&=E_2 \\ -R_5I_1+(R_2+R_4+R_5)I_2+R_4I_3&=E_2 \end{aligned}
よって答えは(ヲ)の\(R_4\)です。
網目方程式(3)
同様の右下のループについて考えます。
\begin{aligned} R_6(I_1+I_3)+R_3I_3+R_4(I_2+I_3)&=E_3 \\ R_6I_1+R_4I_2+(R_3+R_4+R_6)I_3&=E_3 \end{aligned}
よって答えは(イ)の\(\displaystyle R_3+R_4+R_6\)です。
ここまでをまとめると
\begin{aligned} \begin{pmatrix} R_1+R_5+R_6 & -R_5 & R_6 \\ -R_5 & R_2+R_4+R_5 & R_4 \\ R_6 & R_4 & R_3+R_4+R_6 \end{pmatrix} \begin{pmatrix} I_1 \\ I_2 \\ I_3 \end{pmatrix} = \begin{pmatrix} E_1-E_2+E_3 \\ E_2 \\ E_3 \end{pmatrix} \end{aligned}
となります。
抵抗が\(R\)の時の\(I_1\)
問題にある条件、\(R_1=R_2=R_3=R_4=R_5=R_6=R\)を適用とすると行列式は以下のようになります。
\begin{aligned} \begin{pmatrix} 3R & -R & R \\ -R & 3R & R \\ R & R & 3R \end{pmatrix} \begin{pmatrix} I_1 \\ I_2 \\ I_3 \end{pmatrix} = \begin{pmatrix} E_1-E_2+E_3 \\ E_2 \\ E_3 \end{pmatrix} \end{aligned}
後はこれを解くだけです。クラメルの公式で解くのが一番速そうですが、本番で分からなくなった時の最終手段としてここでは連立方程式でやります。
\begin{cases} 3RI_1-RI_2+RI_3 = E_1-E_2+E_3 \quad & (1) \\ -RI_1+3RI_2+RI_3 = E_2 \quad & (2) \\ RI_1+RI_2+3RI_3 = E_3 \quad & (3) \end{cases}
\begin{cases} 3I_1 - I_2 + I_3 = \dfrac{E_1-E_2+E_3}{R} \quad & (4) \\ -I_1 + 3I_2 + I_3 = \dfrac{E_2}{R} \quad & (5) \\ I_1 + I_2 + 3I_3 = \dfrac{E_3}{R} \quad & (6) \end{cases}
(5)式と(6)式を足して \(I_1\) を消去します。
\begin{aligned} (-I_1+3I_2+I_3) + (I_1+I_2+3I_3) &= \frac{E_2}{R} + \frac{E_3}{R} \\ 4I_2 + 4I_3 &= \frac{E_2+E_3}{R} \\ I_2 + I_3 &= \frac{E_2+E_3}{4R} \quad (7) \\ \end{aligned}
3 × (5)式 と (4)式を足して \(I_1\) を消去します。
\begin{aligned} 3(-I_1+3I_2+I_3) + (3I_1-I_2+I_3) &= 3\frac{E_2}{R} + \frac{E_1-E_2+E_3}{R} \\ (-3I_1+9I_2+3I_3) + (3I_1-I_2+I_3) &= \frac{3E_2 + E_1-E_2+E_3}{R} \\ 8I_2 + 4I_3 &= \frac{E_1+2E_2+E_3}{R} \quad (8) \\ \end{aligned}
(7)式から \(I_3 = \dfrac{E_2+E_3}{4R} - I_2\) とし、(8)式に代入します。
\begin{aligned} 8I_2 + 4\left(\frac{E_2+E_3}{4R} - I_2\right) &= \frac{E_1+2E_2+E_3}{R} \\ 8I_2 + \frac{E_2+E_3}{R} - 4I_2 &= \frac{E_1+2E_2+E_3}{R} \\ 4I_2 &= \frac{E_1+2E_2+E_3 - (E_2+E_3)}{R} \\ 4I_2 &= \frac{E_1+E_2}{R} \\ I_2 &= \frac{E_1+E_2}{4R} \\ \end{aligned}
\(I_2\) の値を(7)式に代入して \(I_3\) を求めます。
\begin{aligned} \frac{E_1+E_2}{4R} + I_3 &= \frac{E_2+E_3}{4R} \\ I_3 &= \frac{E_2+E_3}{4R} - \frac{E_1+E_2}{4R} \\ I_3 &= \frac{E_2+E_3 - E_1 - E_2}{4R} \\ I_3 &= \frac{-E_1+E_3}{4R} \\ \end{aligned}
\(I_2\) と \(I_3\) の値を(6)式に代入して \(I_1\) を求めます。
\begin{aligned} I_1 + \left(\frac{E_1+E_2}{4R}\right) + 3\left(\frac{-E_1+E_3}{4R}\right) &= \frac{E_3}{R} \\ I_1 &= \frac{4E_3}{4R} - \frac{E_1+E_2}{4R} - \frac{-3E_1+3E_3}{4R} \\ I_1 &= \frac{4E_3 - E_1 - E_2 + 3E_1 - 3E_3}{4R} \\ I_1 &= \frac{2E_1-E_2+E_3}{4R} \\ \end{aligned}
結果をまとめると以下となります。
\begin{cases} I_1 = \dfrac{2E_1 - E_2 + E_3}{4R} \\ I_2 = \dfrac{E_1 + E_2}{4R} \\ I_3 = \dfrac{-E_1 + E_3}{4R} \end{cases}
よって答えは(ル)の\(\displaystyle \frac{2E_1-E_2+E_3}{4R}\)です。
抵抗が\(R\)の時の\(I_4\)
図より、\(I_4=I_2+I_3\)なので
\begin{align*} I_4 &= I_2 + I_3 \\ &= \frac{E_1 + E_2}{4R} + \frac{-E_1 + E_3}{4R} \\ &= \frac{(E_1 + E_2) + (-E_1 + E_3)}{4R} \\ &= \frac{E_1 + E_2 - E_1 + E_3}{4R} \\ &= \frac{E_2 + E_3}{4R} \end{align*}
よって答えは(カ)の\(\displaystyle \frac{E_2+E_3}{4R}\)です。
- (1)ロ \(R_1+R_5+R_6\)
- (2)ヲ \(R_4\)
- (3)イ \(\displaystyle R_3+R_4+R_6\)
- (4)ル \(\displaystyle \frac{2E_1-E_2+E_3}{4R}\)
- (5)カ \(\displaystyle \frac{E_2+E_3}{4R}\)