電験一種 H26年 理論 問2
次の文章は, 導体及び抵抗体周辺における電界・磁界に関する記述である。文中の(0) に当てはまる最も適切なものを解答群の中から選びなさい。
導体Aと導体Bの間に円柱状の抵抗体が挿入されており, 導体Aから導体Bに向かって直流電流\(I\)が一様に流れている図1のような状態を考える。ここで, 導体Aの電位\(V_A\)と導体Bの電位\(V_B\)は\(V_A > V_B > 0\)とし, 導体A, Bでの電圧降下は零とする。
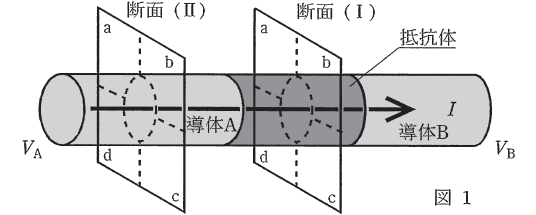
このとき, 図中の断面(I)において, 断面と垂直な方向の電界成分を模式的に描いたものとしてふさわしいのは(1)である。また, 断面と平行な方向の磁界成分を磁力線を用いて模式的に描いたものとしてふさわしいのは(2)である。
ポインティングベクトル\(\vec{S}\)は電界\(\vec{E}\)及び磁界\(\vec{H}\)を用いて\(\vec{S} = \vec{E} \times \vec{H}\)と表されるため, 断面(I)における断面と平行な方向のポインティングベクトルの様子を模式的に描くと, (3) のようになる。
次に, 断面(II)における断面と平行な方向の電界成分を電気力線を用いて模式的に描いたものとしてふさわしいのは(4)である。断面と平行な方向の磁界成分を磁力線を用いて模式的に描いたものとしてふさわしいのは(2)なので, 断面と垂直な方向のポインティングベクトルの様子を模式的に描くと(5)のようになる。
このように, ポインティングベクトルを用いてエネルギーの流れを考察すると, 抵抗体周辺の空間から抵抗体に向けてエネルギーの一部が流入していることが分かる。
なお, 解答群(1)〜(3)の図において, \(\bigotimes\)は図1において左から右に断面を横切る向きを, \(\bigodot\)は図1において右から左に断面を横切る向きを示す。また, 円の内部に何も記していないものは, その成分が導体内あるいは抵抗体内で零であることを意味している。導体A, Bは十分長いものとし, 電位\(V_A, V_B\)の基準としては, 導体A, Bと同軸で半径が十分大きい円筒の電位を零とする。
| (イ) | 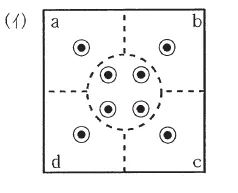 |
(ロ)(1) | 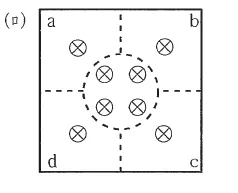 |
(ハ) | 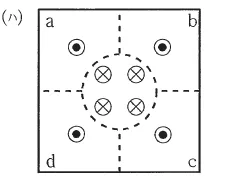 |
| (ニ) | 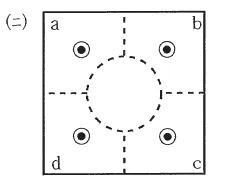 |
(ホ)(5) | 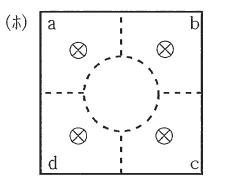 |
(ヘ) | 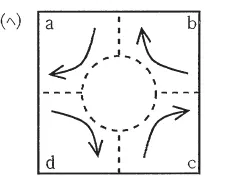 |
| (ト) | 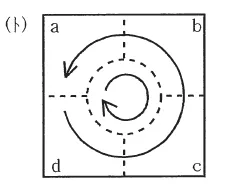 |
(チ)(2) | 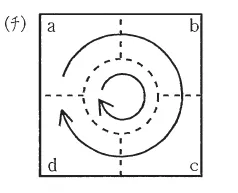 |
(リ) | 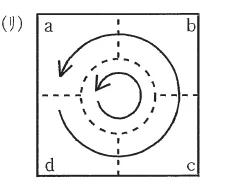 |
| (ヌ) | 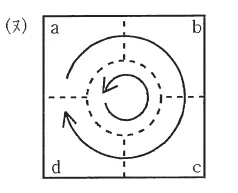 |
(ル) | 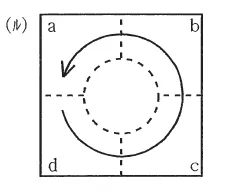 |
(ヲ)(3) | 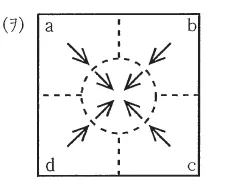 |
| (ワ)(4) | 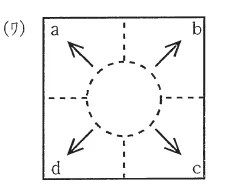 |
(カ) | 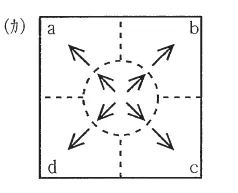 |
(ヨ) | 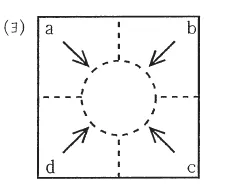 |
出典:平成26年度第一種電気主任技術者理論科目A問題問2
解説
ポインティングベクトルの理解に役立つ問題かと思います。
断面(I)に垂直な方向の電界成分
問題にあるように\(V_A \gt V_B \gt 0 \)なので抵抗体の部分には電位差があります。よって電界が存在します。
この電界は電位の高いところから低いところに向かうので、解答群の場合は紙面の奥へ向かう方向となります。
点電荷の場合を考えれば分かりやすいかと思いますが、これは抵抗内部だけでなく外部にも存在し、いずれにせよ紙面の奥へ向かう方向です。(そもそも選択肢に外部に電界がないパターンはありませんが)
よって答えは(ロ)です。
断面(I)に平行な方向の磁界成分
右ネジの法則より答えは(チ)です。
選択肢的に右ネジの法則だけ覚えていれば正答を選べるかと思います。
断面(I)における断面と平行な方向のポインティングベクトル
問題に\(\vec{S} = \vec{E} \times \vec{H}\)とある通り(1)の電界と(2)の磁界から考えると\(\vec{S}\)は中心に向かう方向となるので答えは(ヲ)です。
分からない場合、\(\vec{F} = \vec{I} \times \vec{B}\)からフレミングの左手の法則で考えるか、ポインティングベクトルが外部から抵抗の方に向かいそれがジュール熱として消費されると暗記しておくかだと思います。
これについて詳しく知りたい場合は専門書が必要ですが、とりあえず問題解くだけであればこの理解で可能です。
断面(II)に平行な方向の電界成分
導体内部においては電位が一定であるため電界は存在していません。一方、外部は導体から離れるほど電位は低下するため、外向きの電界が存在することになります。
これを示している図は(ワ)です。
なお、電流の分布は同じなので磁界の成分は変わりません。
断面(II)に垂直な方向のポインティングベクトル
(3)と同様に\(\vec{S} = \vec{E} \times \vec{H}\)から考えますとポインティングベクトルは紙面の奥に向かう方向となります。
ただし、導体の内部に電界はありませんのでポインティングベクトルも内部には存在しません。
これを示した図は(ホ)となります。
- (1)ロ

- (2)チ

- (3)ヲ

- (4)ワ

- (5)ホ
