電験一種 H26年 理論 問1
次の文章は, 誘電体が挿入された平行平板コンデンサに関する記述である。文中の(0) に当てはまる最も適切なものを解答群の中から選びなさい。
空気中に平行平板コンデンサがある。極板は一辺の長さが\(a\)の十分薄い正方形の導体平板であり, その極板間の距離は\(d\)である。なお, 空気の誘電率を真空と同じ\(\varepsilon_0\)とし, 端効果はないものとする。
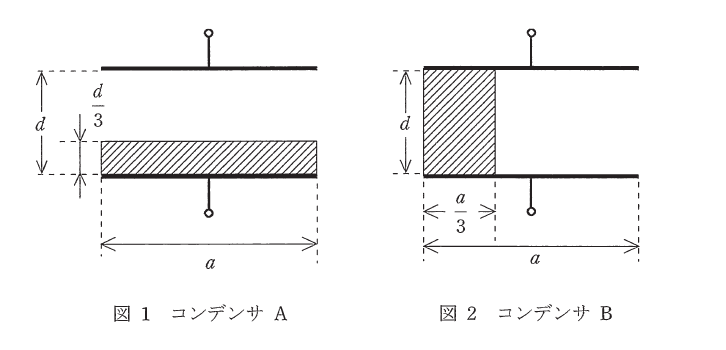
このコンデンサに, 図1のように, 各辺が\(a, a, \dfrac{d}{3}\)の直方体で比誘電率が4の誘電体を, 極板からはみ出さないように挿入したものをコンデンサAとする。
また, 図2のように, コンデンサAの誘電体と同体積かつ同種の誘電体を\(a\), \(\dfrac{a}{3}\), \(d\)の直方体の誘電体を極板からはみ出さないように挿入したものをコンデンサBとする。ただし, 図1, 2とも横から見た図である。
コンデンサAに電荷を与えたとき, 誘電体中と空気中において (1) が等しくなる。また, コンデンサAとBの静電容量は, それぞれ (2) と (3) である。
ここで, 電界強度が\(E\)を超えると, 使用した誘電体では絶縁破壊が起きるが, 空気では絶縁破壊が起きないものとする。このとき, コンデンサAとBの中の誘電体が絶縁破壊を起こさずに端子間に印加できる最大電圧は, それぞれ (4) と \(Ed\) である。したがって, 各コンデンサに最大電圧を与えた際に蓄えられる静電エネルギーは, (5) 。
| (イ) | \(\displaystyle \frac{4\varepsilon_0 a^2}{d}\) | (ロ)(2) | \(\displaystyle \frac{4\varepsilon_0 a^2}{3d}\) | (ハ) | Bの方が大きい |
| (ニ) | \(Ed\) | (ホ) | 分極 | (ヘ)(1) | 電束密度 |
| (ト)(4) | \(3Ed\) | (チ) | 同じである | (リ) | \(\displaystyle \frac{3\varepsilon_0 a^2}{d}\) |
| (ヌ)(3) | \(\displaystyle \frac{2\varepsilon_0 a^2}{d}\) | (ル) | \(\displaystyle \frac{6\varepsilon_0 a^2}{5d}\) | (ヲ) | \(4Ed\) |
| (ワ) | 電界 | (カ) | \(\displaystyle \frac{3\varepsilon_0 a^2}{2d}\) | (ヨ)(5) | Aの方が大きい |
出典:平成26年度第一種電気主任技術者理論科目A問題問1
解説
簡単な問題であり、他の受験者も高得点であろうことを考えるとしっかり正答したい問題です。
コンデンサAで誘電体中と空気中において等しいもの
多分答えを出すだけなら一種受験者ならすぐかと思います。答えは(ヘ)の電束密度です。
電束密度は誘電率によらないのでどちらも電束密度は等しくなります。
ここらへんの詳しい話は専門書の方がいいかと思います。
コンデンサAの静電容量
コンデンサAの静電容量\(C_A\)は、間隔\(\dfrac{2d}{3}\)のコンデンサと間隔\(\dfrac{d}{3}\)で比誘電率4のコンデンサとの直列接続なので
\begin{aligned} C_A &= \dfrac{\dfrac{3\varepsilon_0 a^2}{2d} \cdot \dfrac{12\varepsilon_0 a^2}{d}}{\dfrac{3\varepsilon_0 a^2}{2d} + \dfrac{12\varepsilon_0 a^2}{d}} \\ &= \dfrac{4\varepsilon_0 a^2}{3d} \\ \end{aligned}
となりますので、答えは(ロ)の\(\displaystyle \frac{4\varepsilon_0 a^2}{3d}\)です。
コンデンサBの静電容量
コンデンサBの静電容量\(C_B\)は、面積\(\dfrac{2a^2}{3}\)のコンデンサと面積\(\dfrac{a^2}{3}\)で比誘電率4のコンデンサとの並列接続なので
\begin{aligned} C_B &= \frac{2\varepsilon_0 a^2}{3d} + \frac{4\varepsilon_0 a^2}{3d} \\ &= \frac{2\varepsilon_0 a^2}{d} \\ \end{aligned}
となりますので、答えは(ヌ)の\(\displaystyle \frac{2\varepsilon_0 a^2}{d}\)です。
コンデンサAに印加できる最大電圧
問題文に「空気では絶縁破壊が起きないものとする」とあることから誘電体の電界が\(E\)の時が端子間に印加できる最大電圧であることが分かります。
この時の電束密度は
\begin{aligned} D &= 4 \varepsilon_0 E \\ \end{aligned}
です。これは空気中でも変わりませんので、空気中の電界は
\begin{aligned} \dfrac{D}{\varepsilon_0} &= 4 E \\ \end{aligned}
となります。端子間に印加できる最大電圧\(V_A\)は
\begin{aligned} V_A &= 4 E \cdot \dfrac{2d}{3} + E \dfrac{d}{3} \\ &= 3Ed \\ \end{aligned}
となりますので、答えは(ト)の\(3Ed\)です。
最大電圧が与えられた時に蓄えられる静電エネルギーの比較
コンデンサAに印加できる最大電圧は\(3Ed\)、コンデンサBに印加できる最大電圧は\(Ed\)と分かっていますのでこれで静電エネルギー\(W_A\)と\(W_B\)を計算します。
\begin{aligned} W_A &= \dfrac{1}{2} \cdot \frac{4\varepsilon_0 a^2}{3d} \cdot \left(3Ed\right)^2\\ &= 6 \varepsilon_0 a^2 E^2 d\\ \end{aligned}
\begin{aligned} W_B &= \dfrac{1}{2} \cdot \frac{2\varepsilon_0 a^2}{d} \cdot \left(Ed\right)^2\\ &= \varepsilon_0 a^2 E^2 d\\ \end{aligned}
よって蓄えられる静電エネルギーはAの方が大きいので、答えは(ヨ)です。
- (1)ヘ 電束密度
- (2)ロ \(\displaystyle \frac{4\varepsilon_0 a^2}{3d}\)
- (3)ヌ \(\displaystyle \frac{2\varepsilon_0 a^2}{d}\)
- (4)ト \(3Ed\)
- (5)ヨ Aの方が大きい