電験一種 H25年 理論 問6
次の文章は、電流が作る磁界に関する記述である。文中の(0)に当てはまるものを解答群の中から選びなさい。
透磁率\(\mu_{0}\)の真空中において、半径\(R\)の円環状の回路に流れる電流\(I\)が円環中心点に作る磁束密度の大きさは(1)である。これを、ビオ・サバールの法則を用いて導出することを考える。
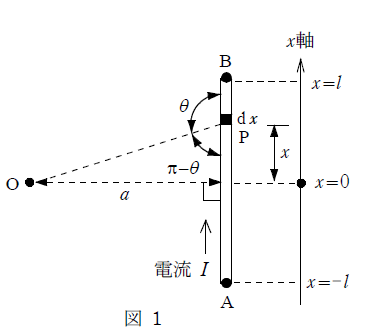
まず、図1に示すような長さ\(2l\)の線分A-Bの部分を流れる電流\(I\)が点Oにもたらす磁界の大きさを求める。このとき、点Oは点A及び点Bから等距離にあり、線分A-Bから距離\(a\)の位置にあるとする。また、線分A-B上に図1に示すように\(x\)軸を考える。
線分A-B上の点Pについて、\(x\)を\(a\)と\(\theta\)を用いて表すと、\(x = \)(2)と表すことができる。このとき、\(\cos\theta=-\cos(\pi-\theta)\)であることなどを参考とされたい。よって、これを\(\theta\)で微分することにより、次式を得る。
\( \dfrac{d x}{d \theta} = \)(3)
ここで、微小部分\(dx\)を流れる電流\(I\)が点Oに作る磁束密度は、線分O-Pの長さを\(r\)とすると、ビオ・サバールの法則により、次式で与えられる。
\(\displaystyle d B=\dfrac{\mu_{0}}{4\pi}\dfrac{I d x \sin \theta}{r^{2}}=\dfrac{\mu_{0}I}{4\pi}\) (4)\(d \theta \)
\(\angle OAB=\angle OBA=\theta_{1}\)とすると、線分A-B全体を流れる電流\(I\)が点Oに作る磁束密度は、これを積分して、次式のように求まる。
\(\displaystyle B_{AB}=\int_{\theta_{1}}^{\pi-\theta_{1}}\dfrac{\mu_{0}I}{4\pi}\)(4)\(d \theta = \)(5)
ただし、\(\cos\theta_{1}=\dfrac{l}{\sqrt{a^{2}+l^{2}}}\)であることを用いた。
次にこれを用いて、図2に示すような、半径\(R\)の円に内接する正\(n\)角形状の電気回路に流れる電流\(I\)が、その中心点Oに作る磁束密度を求める。
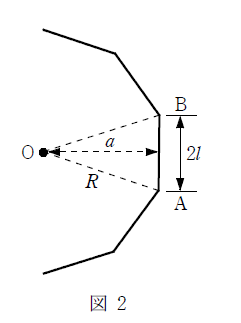
線分A-Bの部分が点Oに作る磁束密度\(B_{AB}\)を\(R\)により表すことを考える。このとき、求めた結果において、\(a=R\cos\dfrac{\pi}{n}\)、\(l=R\sin\dfrac{\pi}{n}\)と表すことができるから、\(B_{AB}=\dfrac{\mu_{0}I}{2\pi R}\tan\dfrac{\pi}{n}\)と求まる。
よって、これを\(n\)倍することで、正\(n\)角形状の電気回路に流れる電流\(I\)が中央に作る磁束密度\(B_{total}\)を求めることができる。ここで、\(n \to \infty\)の極限値を考えると、\(B_{total} = \)(1)となり、円環状の回路に流れる電流が中心点に作る磁束密度の大きさと一致する。このとき、\( \lim_{n\to\infty}\dfrac{n}{\pi}\tan\dfrac{\pi}{n}=1 \)であることを用いた。
| (イ) | \(a\sin\theta\) | (ロ)(1) | \(\displaystyle \frac{\mu_0I}{2R}\) | (ハ) | \(-a\displaystyle \frac{\sin\theta}{\cos\theta}\) | (ニ)(2) | \(-a\displaystyle \frac{\cos\theta}{\sin\theta}\) |
| (ホ) | \(\displaystyle \frac{I}{2\pi R}\) | (ヘ) | \(-\displaystyle \frac{a}{\cos^2\theta}\) | (ト) | \(\displaystyle \frac{\mu_0I}{2\pi R}\) | (チ)(3) | \(\displaystyle \frac{a}{\sin^2\theta}\) |
| (リ)(5) | \(\displaystyle \frac{\mu_0Il}{2\pi a\sqrt{a^2+l^2}}\) | (ヌ) | \(a\cos\theta\) | (ル) | \(\displaystyle \frac{\mu_0Il^2}{4\pi a(a^2+l^2)}\) | (ヲ) | \(\displaystyle \frac{\cos^2\theta}{a}\) |
| (ワ)(4) | \(\displaystyle \frac{\sin\theta}{a}\) | (カ) | \(\displaystyle \frac{\cos\theta}{a}\) | (ヨ) | \(\displaystyle \frac{\mu_0Il}{4\pi a\sqrt{a^2+l^2}}\) |
出典:平成25年度第一種電気主任技術者理論科目B問題問6
解説
B問題問7の方が明らかに簡単なので本番でこれを選ぶかは疑問ですが、過去問はやっておきましょう。
透磁率\(\mu_{0}\)の真空中において、半径\(R\)の円環状の回路に流れる電流\(I\)が円環中心点に作る磁束密度の大きさ
透磁率\(\mu_{0}\)の真空中において、半径\(R\)の円環状の回路に流れる電流\(I\)が円環中心点に作る磁束密度の大きさは\(\displaystyle \frac{\mu_0I}{2R}\)です。
よって答えは(ロ)の\(\displaystyle \frac{\mu_0I}{2R}\)です。
なお、ここの誤答用選択肢は(ホ)の\(\displaystyle \frac{I}{2\pi R}\)と(ト)の\(\displaystyle \frac{\mu_0I}{2\pi R}\)になると思いますが、これは直線電流による磁場の強さと磁束密度です。
線分A-B上の点Pについて、\(x\)を\(a\)と\(\theta\)を用いて表す
図より、\(a=x \tan\left(\pi - \theta \right) \)です。
しかし、これは解答の選択肢にありませんので解答の選択肢になるように変形します。
\begin{aligned} a&=x \tan\left(\pi - \theta \right) \\ &= x \dfrac{\sin \left(\pi - \theta \right)}{\cos \left(\pi - \theta \right)} \end{aligned}
ここで、\(\sin \left(\pi - \theta \right) = \sin \theta \)、\(\cos \left(\pi - \theta \right) = - \cos \theta \)なので、
\begin{aligned} a &= x \dfrac{\sin \left(\pi - \theta \right)}{\cos \left(\pi - \theta \right)} \\ &= x \dfrac{\sin \pi }{- \cos \pi } \end{aligned}
\begin{aligned} x &= - a \dfrac{\cos \theta }{ \sin \theta} \\ \end{aligned}
よって答えは(ニ)の\(-a\displaystyle \frac{\cos\theta}{\sin\theta}\)です。
\(x\)を\(\theta\)で微分する
微分するだけなので特別難しいことはなく微分を覚えているか否かだけです。
商の微分公式 \(\left(\dfrac{u}{v}\right)' = \dfrac{u'v - uv'}{v^2}\) を適用します。
\begin{aligned} \frac{dx}{d\theta} &= -a \dfrac{(-\sin \theta)(\sin \theta) - (\cos \theta)(\cos \theta)}{\sin^2 \theta} \\ &= a \dfrac{\sin^2 \theta + \cos^2 \theta}{\sin^2 \theta} \\ &= \dfrac{a}{\sin^2 \theta} \\ \end{aligned}
よって答えは(チ)の\(\displaystyle \frac{a}{\sin^2\theta}\)です。
微小部分\(dx\)を流れる電流\(I\)が点Oに作る磁束密度
問題文で以下の式が与えられています。
\begin{aligned} \mathrm{d}B &= \dfrac{\mu_0}{4\pi} \frac{I \mathrm{d}x \sin \theta}{r^2} \\ \end{aligned}
まずは(3)の答えを代入します。
\begin{aligned} \mathrm{d}B &= \dfrac{\mu_0}{4\pi} \frac{I \mathrm{d}x \sin \theta}{r^2} \\ &= \dfrac{\mu_0}{4\pi} \frac{I \sin \theta}{r^2} \cdot \frac{a}{\sin^2\theta} \mathrm{d}\theta \\ &= \dfrac{\mu_0}{4\pi} \frac{I }{r^2} \cdot \frac{a}{\sin\theta} \mathrm{d}\theta \\ \end{aligned}
選択肢には上記は存在しないため、まずは\(r\)を消去します。\(r\)は線分O-Pなので、\(r = \sqrt{a^2 + x^2} \)で表されます。よって
\begin{aligned} \mathrm{d}B &= \dfrac{\mu_0}{4\pi} \frac{I }{a^2 + x^2} \cdot \frac{a}{\sin\theta} \mathrm{d}\theta \\ \end{aligned}
となります。しかし、これも選択肢にはないので更に\(x\)を消去します。
※問題文の少し後に若干ヒントになる\(\cos\)の式があります。
\begin{aligned} \sin \left( \pi - \theta \right) &= \sin \theta = \dfrac{a}{\sqrt{a^2 + x^2}} \\ \end{aligned}
なので
\begin{aligned} \sin^2 \theta = \dfrac{a^2}{a^2 + x^2} \\ \end{aligned}
であり、よって
\begin{aligned} \dfrac{a}{a^2 + x^2} &= \dfrac{\sin^2 \theta}{a} \\ \end{aligned}
です。更にこれを代入します。
\begin{aligned} \mathrm{d}B &= \dfrac{\mu_0}{4\pi} \frac{I }{a^2 + x^2} \cdot \frac{a}{\sin\theta} \mathrm{d}\theta \\ &= \dfrac{\mu_0}{4\pi} \frac{I }{a} \cdot \frac{\sin^2 \theta}{\sin\theta} \mathrm{d}\theta \\ &= \dfrac{\mu_0 I}{4\pi} \frac{ \sin \theta }{a} \mathrm{d}\theta \\ \end{aligned}
選択肢にある形になりました。答えは(ワ)の\(\displaystyle \frac{\sin\theta}{a}\)です。
線分A-B全体を流れる電流\(I\)が点Oに作る磁束密度
問題文にある通り積分します。
\begin{aligned} B_{AB}&=\int_{\theta_{1}}^{\pi-\theta_{1}}\dfrac{\mu_{0}I}{4\pi} \frac{\sin\theta}{a} \mathrm{d} \theta \\ &= \frac{\mu_0 I}{4\pi a} \int_{\theta_1}^{\pi-\theta_1} \sin \theta \, \mathrm{d}\theta \\ &= \frac{\mu_0 I}{4\pi a} \left[ -\cos \theta \right]_{\theta_1}^{\pi-\theta_1} \\ &= \frac{\mu_0 I}{4\pi a} \left[ -\cos(\pi - \theta_1) - (-\cos \theta_1) \right] \\ &= \frac{\mu_0 I}{4\pi a} \left( \cos\theta_1 +\cos \theta_1\right) \\ &= \frac{\mu_0 I}{2\pi a} \cos\theta_1\\ \end{aligned}
問題文にある\(\cos \theta_1 = \dfrac{l}{\sqrt{a^2+l^2}} \)を代入すると
\begin{aligned} B_{AB}&= \frac{\mu_0 I}{2\pi a} \cos\theta_1\\ &= \frac{\mu_0Il}{2\pi a\sqrt{a^2+l^2}} \\ \end{aligned}
となります。答えは(リ)の\(\displaystyle \frac{\mu_0Il}{2\pi a\sqrt{a^2+l^2}}\)です。
参考:極限値を求めて円環状の回路に流れる電流が中心点に作る磁束密度の大きさを求める
ここまでで(5)まで解き終わっているので本番では考える必要はありませんが、過去問を解く場合は他の問題に対応するためにやっておいて損はないかと思います。
問題文にある\(a = R\cos\left(\dfrac{\pi}{n} \right) \)と\(l = R\sin\left(\dfrac{\pi}{n}\right) \)を用いて式変形します。
\(\sin^2 \theta + \cos^2 \theta = 1\) なので
\begin{aligned} a^2 + l^2 &= \left\{ R\cos\left(\frac{\pi}{n}\right) \right\}^2 + \left\{ R\sin\left(\frac{\pi}{n}\right) \right\}^2 \\ &= R^2 \\ \end{aligned}
です。よって
\begin{aligned} B_{AB}&= \frac{\mu_0Il}{2\pi a\sqrt{a^2+l^2}} \\ &= \frac{\mu_0I R\sin\left(\dfrac{\pi}{n}\right) }{2\pi R\cos\left(\dfrac{\pi}{n} \right) R } \\ &= \frac{\mu_0I }{2\pi R } \tan \dfrac{\pi}{n}\\ \end{aligned}
となります。これの\(n\)倍は
\begin{aligned} B_{total} &= \frac{\mu_0 I }{2\pi R } \tan \dfrac{\pi}{n} \times n\\ &= \frac{\mu_0 I }{2 R } \dfrac{n}{\pi} \tan \dfrac{\pi}{n} \\ \end{aligned}
です。
問題文にある通り\( \lim_{n\to\infty}\dfrac{n}{\pi}\tan\dfrac{\pi}{n}=1 \)なので、上式の極限は\(\displaystyle \frac{\mu_0I}{2R}\)となります。
- (1)ロ \(\displaystyle \frac{\mu_0I}{2R}\)
- (2)ニ \(-a\displaystyle \frac{\cos\theta}{\sin\theta}\)
- (3)チ \(\displaystyle \frac{a}{\sin^2\theta}\)
- (4)ワ \(\displaystyle \frac{\sin\theta}{a}\)
- (5)リ \(\displaystyle \frac{\mu_0Il}{2\pi a\sqrt{a^2+l^2}}\)