電験一種 H25年 理論 問5
次の文章は、三相交流回路に関する記述である。文中の(0)に当てはまるものを解答群の中から選びなさい。ただし、\(a\)は複素数で\(a=e^{j\frac{2}{3}\pi}\)とする。
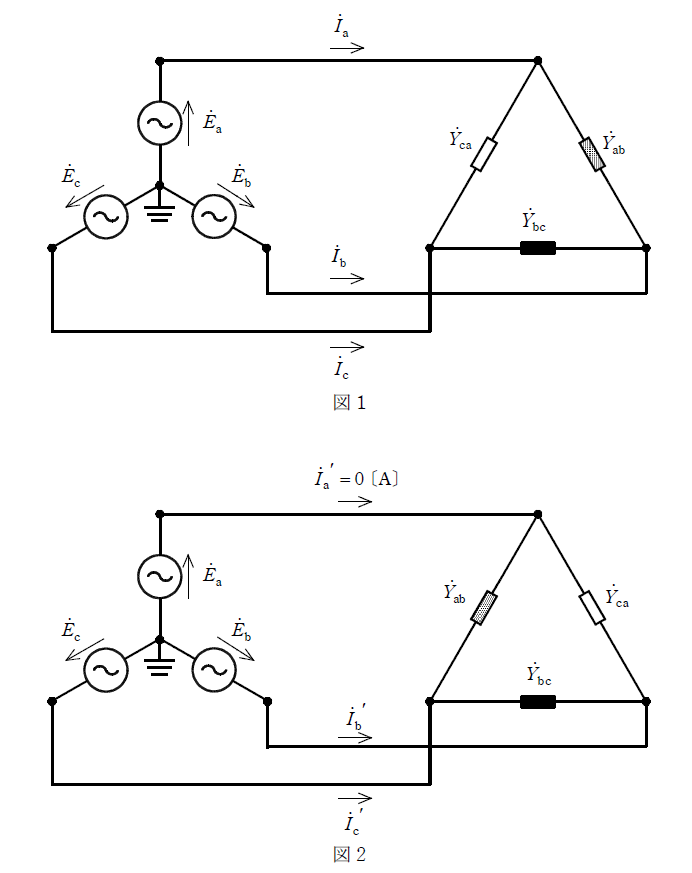
図1と図2に示すように、対称三相交流電源に\(\triangle\)形不平衡負荷を接続した。図1と図2では、\(\triangle\)形不平衡負荷のアドミタンス\(\dot{Y}_{ab}\)、\(\dot{Y}_{bc}\)、\(\dot{Y}_{ca}\)の配置が入れ替わっている。各相の電圧は\(\dot{E}_{a}=100\angle0^{\circ} \text{ [V]}\)に対し、\(\dot{E}_{b}=a^{2}\dot{E}_{a}\)、\(\dot{E}_{c}=a\dot{E}_{a}\)である。図1と図2の\(\triangle\)形不平衡負荷のベクトル(複素)電力をそれぞれ\(\dot{S}_{1}\)、\(\dot{S}_{2}\)とする。このとき、以下の結果を得た。
① 図1の線電流\(\dot{I}_{a}\)は\(\dot{I}_{a}=10(1-a^{2}) \text{ [A]}\)、\(\dot{I}_{b}\)は\(\dot{E}_{b}\)と同相、\(\dot{I}_{c}\)は\(\dot{E}_{a}\)と逆相であった。
② 図2の線電流\(\dot{I}_{a}^{\prime}\)は\(0 \text{ [A]}\)であった。
③ 図1の\(\triangle\)形不平衡負荷のベクトル(複素)電力は\(\dot{S}_{1}=2000(1-a)\) (実部は有効電力\(\text{[W]}\)、虚部は無効電力\(\text{[var]}\))であった。
①の結果にキルヒホッフの電流則を適用し、線電流\(\dot{I}_{a}\)、\(\dot{I}_{b}\)、\(\dot{I}_{c}\)のベクトル図を描くと、\(\dot{I}_{b}\)、\(\dot{I}_{c}\)の値は、\( (\dot{I}_{b},\dot{I}_{c})=\)(1)[A]となる。
②の結果、\(\dot{I}_{a}^{\prime}=0 \text{ [A]}\)より、\(\dot{Y}_{ab} = \)(2)\( \times \dot{Y}_{bc}\)となる。ただし、複素数\(a\)の性質\(a^{3}=1\)、\(1+a+a^{2}=0\)に注意する。この関係式と図1の線電流\(\dot{I}_{a}\)、\(\dot{I}_{b}\)から\(\dot{Y}_{ab}\)、\(\dot{Y}_{bc}\)、\(\dot{Y}_{ca}\)が順次求められる。
一方、③の結果を利用すると、アドミタンスの和\(\dot{Y}_{ab}+\dot{Y}_{bc}+\dot{Y}_{ca}\)の値は、ベクトル(複素)電力\(\dot{S}_{1} = \)(3)\( \times |\dot{E}_{a}|^{2} \overline{(\dot{Y}_{ab}+\dot{Y}_{bc}+\dot{Y}_{ca})} \)の式から直接求めることができる。また、②の結果とキルヒホッフの電流則を利用すると図2のベクトル(複素)電力\(\dot{S}_{2}\)は\(\dot{S}_{2} = \left( \right. \)(4)\(\left. \right) \times \overline{\dot{I}_{c}^{\prime}}\)と表せる。\(\dot{S}_{2}\)の式と③の結果を利用すると、\(\dot{I}_{c}^{\prime} = \) (5)[A]となる。
(注)\( \overline{\dot{Z}}\) は複素数\(\dot{Z}\)の共役複素数を表す。
| (イ) | 1 | (ロ) | \(\dot{E}_c-\dot{E}_a\) | (ハ) | \((20a^2, -10)\) | (ニ) | \(3a\) |
| (ホ)(2) | \(a^2\) | (ヘ) | \((10a^2, -20)\) | (ト)(5) | \(20a\) | (チ)(4) | \(\dot{E}_c-\dot{E}_b\) |
| (リ)(3) | 3 | (ヌ) | \(2a\) | (ル) | \(30a^2\) | (ヲ) | \(25a^2\) |
| (ワ)(1) | \((10a^2, -10)\) | (カ) | \(\dot{E}_a-\dot{E}_b\) | (ヨ) | \(\sqrt{3}\) |
出典:平成25年度第一種電気主任技術者理論科目B問題問5
解説
よくあるタイプの三相交流の問題です。確実に解けるようにしておきたいです。
\(\dot{I}_{b}\)、\(\dot{I}_{c}\)の値
キルヒホッフの電流測より\( \dot I_{a}+\dot I_{b}+\dot I_{c}=0 \)です。
問題文より、\(\dot I_{b}\)は\(a^2\)に比例します。また、\(\dot I_{c}\)は実数です。
ここで、\(\dot{I}_{b}=ka^2\)、\(\dot I_{c}=R\)として上の式を計算します。
\begin{aligned} \dot I_{a}+\dot I_{b}+\dot I_{c} &= 0 \\ 10(1-a^{2}) + ka^2 + R &= 0 \\ (R+10) + (k-10)a^2 &= 0 \\ \end{aligned}
上の式が成り立つためには\(R+10=0\)、\(k-10=0\)でないといけませんから、
\begin{aligned} R &=-10 \\ k &=10 \\ \end{aligned}
となることが分かります。よって\(\dot{I}_{b}=10a^2\)、\(\dot I_{c}=-10\)です。
以上より、\( (\dot{I}_{b},\dot{I}_{c})=(10a^2, -10)\)であり、答えは(ワ)の\((10a^2, -10)\)です。
\(\dot{Y}_{ab} \)と\(\dot{Y}_{ca} \)の関係
\(\dot{I}_{a}^{\prime}\)は\(\dot{Y}_{ab} \)と\(\dot{Y}_{ca} \)を流れる電流の和になります。向きに注意して式を立てますと
\begin{aligned} \dot{I}_{a}^{\prime} = \dot{Y}_{ab} \left( \dot{E}_{a} - \dot{E}_{b} \right) + \dot{Y}_{ca} \left( \dot{E}_{a} - \dot{E}_{c} \right)\\ \end{aligned}
となります。これらに\(\dot{I}_{a}^{\prime}=0\)、\(\dot{E}_{a}=100\)、\(\dot{E}_{b}=100a^2\)、\(\dot{E}_{c}=100a\)を代入して整理します。
\begin{aligned} 0 &= \dot{Y}_{ab} \left(100 - 100a^2 \right) + \dot{Y}_{ca} \left( 100 - 100a \right)\\ 0 &= \dot{Y}_{ab} \left(1 - a^2 \right) + \dot{Y}_{ca} \left( 1 - a \right) \\ \dot{Y}_{ab} &= \dfrac {a^2 -1}{1-a} \dot{Y}_{ca} \\ \end{aligned}
分母と分子を整理します。
\begin{aligned} \dot{Y}_{ab} &= \dfrac {a^2 -1}{1-a} \dot{Y}_{ca} \\ &= \dfrac {\left( a+ 1\right)\left( a - 1\right)}{1-a} \dot{Y}_{ca} \\ &= - \dfrac {\left( a+ 1\right)\left( 1-a \right)}{1-a} \dot{Y}_{ca} \\ &= - \left( a+ 1\right) \dot{Y}_{ca} \\ \end{aligned}
\(1+a+a^{2}=0\)を利用して整理します。\(1+a=-a^{2}\)なので
\begin{aligned} \dot{Y}_{ab} &= - \left( a+ 1\right) \dot{Y}_{ca} \\ &= - \left( -a^{2} \right) \dot{Y}_{ca} \\ &= a^{2} \dot{Y}_{ca} \\ \end{aligned}
よって答えは(ホ)の\(a^2\)です。
ベクトル(複素)電力\(\dot{S}_{1} \)
遅れ無効電力を正として複素電力を求めます。各アドミタンスを流れる電流を\(\dot{I}_{xy}\)とします。複素電力は各電流の共役複素数とアドミタンスにかかる電圧との積の和です。
\begin{aligned} \dot{S}_1 &= (\dot{E}_a - \dot{E}_b)\overline{\dot{I}_{ab}} + (\dot{E}_b - \dot{E}_c)\overline{\dot{I}_{bc}} + (\dot{E}_c - \dot{E}_a)\overline{\dot{I}_{ca}} \\ \end{aligned}
\(\dot{E}_b = a^2\dot{E}_a\)、\(\dot{E}_c = a\dot{E}_a\)、および\(\dot{I}_{xy} = \dot{Y}_{xy}(\dot{E}_x - \dot{E}_y)\) を代入します。
\begin{aligned} \dot{S}_1 &= (\dot{E}_a - a^2\dot{E}_a)\overline{\dot{Y}_{ab}(\dot{E}_a - \dot{E}_b)} + (a^2\dot{E}_a - a\dot{E}_a)\overline{\dot{Y}_{bc}(\dot{E}_b - \dot{E}_c)} + (a\dot{E}_a - \dot{E}_a)\overline{\dot{Y}_{ca}(\dot{E}_c - \dot{E}_a)} \\ &= (\dot{E}_a - a^2\dot{E}_a)\overline{\dot{Y}_{ab}(\dot{E}_a - a^2\dot{E}_a)} + (a^2\dot{E}_a - a\dot{E}_a)\overline{\dot{Y}_{bc}(a^2\dot{E}_a - a\dot{E}_a)} + (a\dot{E}_a - \dot{E}_a)\overline{\dot{Y}_{ca}(a\dot{E}_a - \dot{E}_a)} \\ &= \dot{E}_a \overline{\dot{E}_a} (1-a^2)\overline{(1-a^2)} \overline{\dot{Y}_{ab}} + \dot{E}_a \overline{\dot{E}_a} (a^2-a) \overline{(a^2-a) }\overline{\dot{Y}_{bc}} + \dot{E}_a \overline{\dot{E}_a} (a-1)\overline{(a-1)} \overline{\dot{Y}_{ca}} \\ \end{aligned}
\(\overline{a^2}=a\)、\(\overline{a}=a^2\)なので
\begin{aligned} \dot{S}_1 &= \dot{E}_a \overline{\dot{E}_a} (1-a^2)(1-a)\overline{\dot{Y}_{ab}} + \dot{E}_a \overline{\dot{E}_a} (a^2-a)(a-a^2)\overline{\dot{Y}_{bc}} + \dot{E}_a \overline{\dot{E}_a} (a-1)(a^2-1)\overline{\dot{Y}_{ca}} \\ \end{aligned}
各括弧の中身を整理します。\(1+a+a^2=0\)を利用します。
\begin{aligned} (1-a^2)(1-a) &= 1 - a -a^2 +a^3 \\ &= 1 - \left(-1\right) + 1 \\ &= 3 \\ \end{aligned}
\begin{aligned} (a^2-a)(a-a^2) &= a^3 - a^4 -a^2 +a^3 \\ &= 1 - a - a^2 + 1 \\ &= 1 - \left(-1\right) + 1 \\ &= 3 \\ \end{aligned}
\begin{aligned} (a-1)(a^2-1) &= a^3 - a -a^2 + 1 \\ &= 1 - a - a^2 + 1 \\ &= 1 - \left(-1\right) + 1 \\ &= 3 \\ \end{aligned}
よって括弧内は全て3になります。
\begin{aligned} \dot{S}_1 &= 3\dot{E}_a \overline{\dot{E}_a} \overline{\dot{Y}_{ab}} + 3\dot{E}_a \overline{\dot{E}_a}\overline{\dot{Y}_{bc}} + 3 \dot{E}_a \overline{\dot{E}_a} \overline{\dot{Y}_{ca}} \\ \end{aligned}
\( \dot{E}_a \overline{\dot{E}_a} = |\dot{E}_a|^2 \)なので
\begin{aligned} \dot{S}_1 &= 3 |\dot{E}_a|^2 \overline{\dot{Y}_{ab}} + 3 |\dot{E}_a|^2 \overline{\dot{Y}_{bc}} + 3 |\dot{E}_a|^2 \overline{\dot{Y}_{ca}} \\ &= 3|\dot{E}_a|^2 (\overline{\dot{Y}_{ab}} + \overline{\dot{Y}_{bc}} + \overline{\dot{Y}_{ca}}) \\ &= 3|\dot{E}_a|^2 (\overline{\dot{Y}_{ab} + \dot{Y}_{bc} + \dot{Y}_{ca}}) \\ \end{aligned}
となります。よって答えは(リ)の3です。
ベクトル(複素)電力\(\dot{S}_{2}\)
②の結果とキルヒホッフの電流則を利用すると、\(\dot{I}_{a}^{\prime}=0\)なので\(\dot{I}_{b}^{\prime}=-\dot{I}_{c}^{\prime}\)となります。これを利用して複素電力の式を整理します。
複素電力はY結線電源なので各相電圧と線電流の共役の積の和で表せます。
\begin{aligned} \dot{S}_2 &= \dot{E}_a \overline{\dot{I}_{a}^{\prime}} + \dot{E}_b \overline{\dot{I}_{b}^{\prime}} + \dot{E}_c \overline{\dot{I}_{c}^{\prime}} \\ \end{aligned}
これを整理すると
\begin{aligned} \dot{S}_2 &= \dot{E}_a \cdot 0 + \dot{E}_b \left( -\overline{\dot{I}_{c}^{\prime}} \right) + \dot{E}_c \overline{\dot{I}_{c}^{\prime}} \\ &= (\dot{E}_c - \dot{E}_b)\overline{\dot{I}_{c}^{\prime}} \\ \end{aligned}
よって答えは(チ)の\(\dot{E}_c-\dot{E}_b\)です。
参考に、各アドミタンスに流れる電流を用いて計算してみたいと思います。
\begin{aligned} \dot{S}_2 &= (\dot{E}_a - \dot{E}_b)\overline{\dot{I}_{ab}^{\prime}} + (\dot{E}_b - \dot{E}_c)\overline{\dot{I}_{bc}^{\prime}} + (\dot{E}_c - \dot{E}_a)\overline{\dot{I}_{ca}^{\prime}} \\ \end{aligned}
\(\dot{I}_{a}^{\prime}=0\)なので、\(\dot{I}_{ab}^{\prime} = \dot{I}_{ca}^{\prime} \)です。
\begin{aligned} \dot{S}_2 &= (\dot{E}_a - \dot{E}_b)\overline{\dot{I}_{ab}^{\prime}} + (\dot{E}_b - \dot{E}_c)\overline{\dot{I}_{bc}^{\prime}} + (\dot{E}_c - \dot{E}_a)\overline{\dot{I}_{ab}^{\prime}} \\ &= (\dot{E}_a - \dot{E}_a - \dot{E}_b + \dot{E}_c)\overline{\dot{I}_{ab}^{\prime}} + (\dot{E}_b - \dot{E}_c)\overline{\dot{I}_{bc}^{\prime}} \\ &= (\dot{E}_b - \dot{E}_c)\overline{\dot{I}_{bc}^{\prime}} - (\dot{E}_b - \dot{E}_c) \overline{\dot{I}_{ab}^{\prime}} \\ &= (\dot{E}_b - \dot{E}_c)\overline{\dot{I}_{bc}^{\prime} } - \overline{\dot{I}_{ab}^{\prime}} \\ \end{aligned}
\(\overline{\dot{I}_{bc}^{\prime} } - \overline{\dot{I}_{ab}^{\prime}} = \dot{I}_{b}^{\prime} = - \dot{I}_{c}^{\prime}\)なので
\begin{aligned} \dot{S}_2 &= (\dot{E}_b - \dot{E}_c)\overline{\dot{I}_{bc}^{\prime} } - \overline{\dot{I}_{ab}^{\prime}} \\ &= (\dot{E}_b - \dot{E}_c) \left( \overline{-\dot{I}_{c}^{\prime} } \right) \\ &= (\dot{E}_c - \dot{E}_b) \overline{\dot{I}_{c}^{\prime} } \\ \end{aligned}
となり一致しました。
\(\dot{S}_{2}\)の式と③の結果を利用して\(\dot{I}_{c}^{\prime}\)を求める
(3)で以下を求めました。
\begin{aligned} \dot{S}_1 &= 3|\dot{E}_a|^2 (\overline{\dot{Y}_{ab} + \dot{Y}_{bc} + \dot{Y}_{ca}}) \\ \end{aligned}
これは、三相平衡電源の場合、全複素電力は各アドミタンスの総和のみに依存し、その配置には依存しないことを示しています。
よって\(\dot{S}_1=\dot{S}_2\)であることが分かります。これを用いて\(\dot{I}_{c}^{\prime}\)を計算します。\(\overline{\dot{I}_{c}^{\prime}} \)は共役であることと\(a^3=1\)に注意します。
\begin{aligned} \dot{S}_1 &= \dot{S}_2 \\ 2000 \left( 1-a \right) &= (\dot{E}_c - \dot{E}_b) \overline{\dot{I}_{c}^{\prime} }\\ 2000 \left( 1-a \right) &= (a\dot{E}_a - a^2\dot{E}_a) \overline{\dot{I}_{c}^{\prime} }\\ \overline{\dot{I}_{c}^{\prime}} &= \dfrac{2000}{100} \cdot \dfrac{1-a }{a-a^2} \\ \overline{\dot{I}_{c}^{\prime}} &= 20 \cdot \dfrac{1-a }{a\left(1-a\right)} \\ \overline{\dot{I}_{c}^{\prime}} &= \dfrac{20 }{a} \\ \overline{\dot{I}_{c}^{\prime}} &= \dfrac{20 }{a} \cdot a^3\\ \overline{\dot{I}_{c}^{\prime}} &= 20a^2 \\ \dot{I}_{c}^{\prime} &= 20a \\ \end{aligned}
よって答えは(ト)の\(20a\)です。
- (1)ワ \((10a^2, -10)\)
- (2)ホ \(a^2\)
- (3)リ 3
- (4)チ \(\dot{E}_c-\dot{E}_b\)
- (5)ト \(20a\)