電験一種 H25年 理論 問3
次の文章は、RC回路に関する記述である。文中の(0)に当てはまるものを解答群の中から選びなさい。
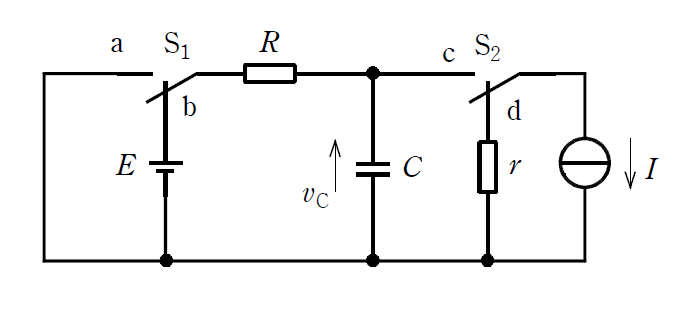
図のようにスイッチ \(S_{1}\)、\(S_{2}\)と直流電圧源\(E\)、直流電流源\(I\)、抵抗\(R\)、\(r\)、静電容量\(C\)が接続されている。静電容量\(C\)の両端の電圧を図のように定める。
時間 \(t \lt 0\) では、スイッチ \(S_{1}\)は\(b\)側、スイッチ \(S_{2}\)は\(d\)側であり、回路は定常状態である。\(t = 0\)において\(S_{1}\)を\(a\)側、\(S_{2}\)を\(c\)側に切り替えた。
\(t \gt 0\)における静電容量\(C\)の両端の電圧\(v_{C}\)の時間的変化について考える。このとき、\(R\)の両端の電圧と\(C\)の両端の電圧は等しいこと、及び初期値を考慮すると、
\( v_{C} = \)(1)
となる。
\(v_{C}\)が\(0 \text{ [V]}\)になった時刻\(T_{1}\)において\(S_{1}\)を\(a\)側から\(b\)側に切り替えた。
\( T_{1} = \)(2)
となる。
\(t \gt T_{1}\)における\(v_{C}\)は、電圧源による過渡応答と電流源による過渡応答との重ね合わせになるので、
\(v_{C} = \)(3) \(+\) (4)
となり、\(t=\infty\)における\(v_{C}\)は(4)となる。(4)\( \gt 0\)のとき、\(v_{C}\)の変化の様子を表す図は(5)である。
| (イ) | \(E-\displaystyle \frac{I}{C}t\) | (ロ)(2) | \(CR\ln\left(1+\displaystyle \frac{E}{RI}\right)\) | (ハ)(1) | \(-RI+(RI+E)e^{-\frac{t}{CR}}\) |
| (ニ) | \(CR\ln\left|\displaystyle \frac{RI}{RI-E}\right|\) | (ホ) | \(E\left(1-e^{-\frac{t}{CR}}\right)\) | (ヘ) | \(RI-E\) |
| (ト)(3) | \(E\left(1-e^{-\frac{t-T_1}{CR}}\right)\) | (チ) | \(Ee^{-\frac{t-T_1}{CR}}\) | (リ)(4) | \(E-RI\) |
| (ヌ) | \(E-RI\left(1-e^{-\frac{t}{CR}}\right)\) | (ル) | \(\displaystyle \frac{EC}{I}\) | (ヲ) | \(E-RI+\displaystyle \frac{I}{C}\) |
| (ワ)(5) | 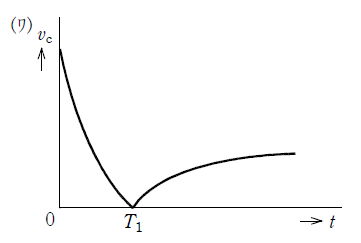 |
||||
| (カ) | 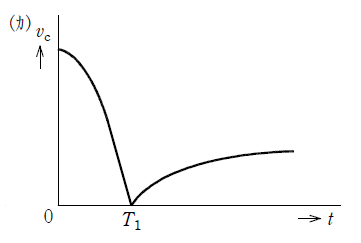 |
||||
| (ヨ) | 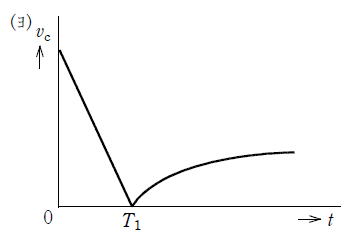 |
||||
出典:平成25年度第一種電気主任技術者理論科目A問題問3
解説
誘導に従えば解ける問題なので得点源としたいところです。
電圧\( v_{C} \)
時間 \(t \lt 0\) では、スイッチ \(S_{1}\)は\(b\)側、スイッチ \(S_{2}\)は\(d\)側なので、初期値は\(E\)であることが分かります。
\(t = 0\)において\(S_{1}\)を\(a\)側、\(S_{2}\)に切り替えると、電流源に\(R\)と\(C\)が並列に接続された回路となります。
並列回路なので、\(R\)にかかっている電圧は\(C\)と等しく\( v_{C} \)です。
これに関する式を立てます。
\(C\)に流れる電流は、図の上の方に電流が流れる時を正とすると\(- C\dfrac {\mathrm {d}v_C}{\mathrm {d}t} \)です。
この電流は抵抗\(R\)と電流源を流れます。よって
\begin{aligned} - C\dfrac {\mathrm {d}v_C}{\mathrm {d}t} &= \dfrac{v_C}{R} + I \\ \end{aligned}
が成り立ちます。
これを解きます。ここではラプラス変換を用いたいと思います。
微分方程式を整理します。
\begin{aligned} \frac{\mathrm {d}v_C}{\mathrm {d}t} + \frac{1}{RC} v_C = - \frac{I}{C} \end{aligned}
ここで、\(\tau = RC\) および \(K = -\dfrac{I}{C}\)とおくと、
\begin{aligned} \frac{\mathrm {d}v_C}{\mathrm {d}t} + \frac{1}{\tau} v_C = K \end{aligned}
\(v_C(t)\) のラプラス変換を \(V_C(s)\) とし、両辺にラプラス変換を適用します。
\begin{aligned} \left\{ s V_C(s) - v_C(0) \right\} + \frac{1}{\tau} V_C(s) &= \frac{K}{s} \\ \left\{ s V_C(s) - E \right\} + \frac{1}{\tau} V_C(s) &= \frac{K}{s} \\ \end{aligned}
これを整理します。
\begin{aligned} V_C(s) \left( s + \frac{1}{\tau} \right) &= E + \frac{K}{s} \\ V_C(s) &= \frac{E}{s + \dfrac{1}{\tau}} + \frac{K}{s \left( s + \dfrac{1}{\tau} \right)} \\ \end{aligned}
第2項を部分分数分解します。
\begin{aligned} V_C(s) &= \frac{E}{s + \dfrac{1}{\tau}} + \left( \dfrac{K \tau}{s} - \dfrac{K \tau}{s + \dfrac{1}{\tau}} \right) \\ V_C(s) &= \frac{K \tau}{s} + \frac{E - K \tau}{s + \dfrac{1}{\tau}} \\ \end{aligned}
逆ラプラス変換します。
\begin{aligned} v_C(t) = K \tau + (E - K \tau) e^{-\frac{t}{\tau}} \end{aligned}
\(K \tau = \left(-\dfrac{I}{C}\right)\left(RC\right) = -RI\) および \(\tau = RC\) を代入します。
\begin{aligned} v_C(t) = -RI + \left(RI+E\right) e^{-\frac{t}{CR}} \end{aligned}
よって答えは(ハ)の\(-RI+(RI+E)e^{-\frac{t}{CR}}\)です。
なお、この問題の場合最終的に\(v_C\)は\(-RI\)にならないといけませんが(\(C\)に流れる電流が0になることから\(C\)には\(RI\)の電圧が加わり、その向きは\(v_C\)の向きとは逆)、初期値\(E\)且つこれを満たすのは解答候補では(ハ)だけなので計算せずとも答えは出せます。これに限らず過渡応答はこの考え方で解ける問題が多いです。
\(v_{C}\)が\(0 \text{ [V]}\)になった時刻\(T_{1}\)
(1)の式に \(v_C(T_1) = 0\)を代入し解きます。
\begin{aligned} 0 &= -RI + (RI + E) e^{-\frac{T_1}{CR}} \\ RI &= (RI + E) e^{-\frac{T_1}{CR}} \\ e^{-\frac{T_1}{CR}} &= \frac{RI}{RI + E} \\ \end{aligned}
両辺の自然対数をとります。
\begin{aligned} - \frac{T_1}{CR} = \ln \left( \frac{RI}{RI + E} \right) \\ \end{aligned}
対数の性質 \(\ln \left(\dfrac{a}{b} \right) = -\ln \left( \dfrac{b}{a} \right)\)を用いて整理します。
\begin{aligned} T_1 &= -CR \ln \left( \frac{RI}{RI + E} \right) \\ &= CR \ln \left( \frac{RI + E}{RI} \right) \\ &= CR \ln \left( 1+ \frac{E}{RI} \right) \end{aligned}
よって答えは(ロ)の\(CR\ln\left(1+\displaystyle \frac{E}{RI}\right)\)です。
\(t \gt T_{1}\)における\(v_{C}\)
\(t \gt T_{1}\)の時、\(S_{1}\)を\(a\)側から\(b\)側に切り替えているので、回路には電圧源と電流源が両方存在する状態となります。
問題にある通り、重ね合わせで考えます。
まず、電流源のみの時、電圧源は短絡で考えます。これは(1)で考えた時の回路と同じです。よって当然答えも同じとなり、問題にある(1)の穴埋め個所がこれを指していることが分かります。
次に電圧源のみの時を考えます。この時、電流源は開放で考えるため、\(E\)に\(R\)と\(C\)が直列に繋がれた回路と解釈することができます。
この時の\(C\)の電圧を\(v_{C1}\)、電流を\(i\)とすると、以下が成り立ちます。
\begin{aligned} E &= v_{C1} + Ri \\ \end{aligned}
ここで、\(i= C\dfrac {\mathrm {d}v_{C1}}{\mathrm {d}t} \)なので
\begin{aligned} E &= v_{C1} + CR\dfrac {\mathrm {d}v_{C1}}{\mathrm {d}t} \\ \end{aligned}
となります。後はこれの\(v_{C1}\)を求めるだけです。
この問題では時間は0から始まらず\(T_1\)から始まるので\(t_1=t-T_1\)とし、\(v_{C1}(t_1)\)として考えます。
電圧源のみを考慮するとき、初期値は0なので\(v_{C1}(0) = 0\)であることに注意してください。
\(v_{C1}(t_1)\)のラプラス変換を\(V_{C1}(s)\)とします。
\begin{aligned} CR \left\{ s V_{C1}(s) - v_{C1}(0) \right\} + V_{C1}(s) &= \frac{E}{s} \\ V_{C1}(s) (CRs + 1) &= \frac{E}{s} \\ V_{C1}(s) &= \frac{E}{s (CRs + 1)} \\ \end{aligned}
分母の\(s\)の係数を\(1\)にするため、分母分子を \(CR\) で割ります。
\begin{aligned} V_{C1}(s) &= \frac{E}{CR} \cdot \frac{1}{s \left( s + \dfrac{1}{CR} \right)} \\ \end{aligned}
部分分数分解します。
\begin{aligned} V_{C1}(s) &= \frac{E}{CR} \left( \frac{CR}{s} - \frac{CR}{s + \dfrac{1}{CR}} \right) \\ &= E \left( \frac{1}{s} - \frac{1}{s + \dfrac{1}{CR}} \right)\\ \end{aligned}
逆ラプラス変換します。
\begin{aligned} v_{C1}(t_1) &= E \left( 1 - e^{-\frac{t_1}{CR}} \right) \\ \end{aligned}
CR回路の過渡応答が出ました。
最初に\(t_1=t-T_1\)としているので、これを代入します。
\begin{aligned} v_{C1}(t) &= E \left( 1 - e^{-\frac{t-T_1}{CR}} \right) \quad (\text{ただし、} t \geqq T_1) \\ \end{aligned}
よって答えは(ト)の\(E\left(1-e^{-\frac{t-T_1}{CR}}\right)\)です。
\(t=\infty\)における\(v_{C}\)
求めた\(v_{C}\)の\(t=\infty\)の時を求めます。
\begin{aligned} v_{C} &= E \left( 1 - e^{-\frac{t-T_1}{CR}} \right) -RI+(RI+E)e^{-\frac{t}{CR}} \\ \end{aligned}
\(t=\infty\)の時\(e^{-\frac{t-T_1}{CR}}\)と\(e^{-\frac{t}{CR}}\)は0になるので、
\begin{aligned} v_{C} &= E \left( 1 - 0 \right) -RI+(RI+E)\cdot 0 \\ &= E- RI \\ \end{aligned}
となります。答えは(リ)の\(E-RI\)です。
\(v_{C}\)の変化の様子を表す図
\(t \gt T_{1}\)以降はどの選択肢も同じなので、\(t \lt T_{1}\)の時のみを考えればいいことが分かります。
その時の\(v_{C}\)の式は\(-RI+(RI+E)e^{-\frac{t}{CR}}\)です。
これは指数関数的に減衰するので、時間の経過とともに変化の度合いが小さくなっているものを選びます。
よって答えは(ワ)です。
- (1)ハ \(-RI+(RI+E)e^{-\frac{t}{CR}}\)
- (2)ロ \(CR\ln\left(1+\displaystyle \frac{E}{RI}\right)\)
- (3)ト \(E\left(1-e^{-\frac{t-T_1}{CR}}\right)\)
- (4)リ \(E-RI\)
- (5)ワ
