電験一種 H25年 理論 問2
次の文章は、直流回路の電流計算 (等価変換) に関する記述である。文中の(0)に当てはまるものを解答群の中から選びなさい。
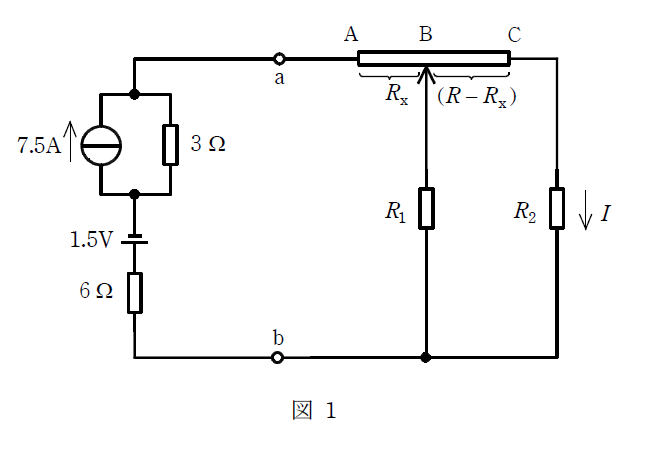
図1において、抵抗 \(R_{2}\) に流れる電流\(I\)が最小になる条件を求めたい。ただし、図の可変抵抗のA-C間の抵抗を\(R\)、A-B間の抵抗を\(R_{x}\)、B-C間の抵抗を\((R-R_{x})\)とする。
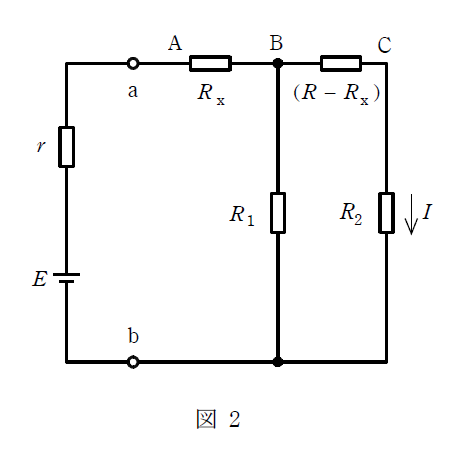
まず、図1の端子a-bより左側部分を図2に示す抵抗\(r\)と電圧源\(E\)に等価変換すると、それぞれ\(r =\)(1) \([\Omega]\)、\(E =\)(2) \([\text{V}]\)となる。
ところで、図2について考えると、\(R_{2}\)に流れる電流\(I\)は、
\(I = \dfrac{R_{1} E}{\boxed{\vphantom{2}\hspace{1em} \text{(3)} \vphantom{2} \hspace{1em}} + R_{1}(R_2+R)+r(R_{1}+R_{2}+R)} \)
となる。ここで、電流\(I\)が最小となる条件は①式の分母が最大の場合であるから、\(R_{x}=\)(4)となるように可変抵抗を調整した場合に電流が最小となる。このとき、\((r+R_{x})\)と\((R-R_{x}+R_{2})\)の関係は、\((r+R_{x})\)(5)\((R-R_{x}+R_{2})\)となる。ただし、\((R_{2}+R) \gt r\)であるとする。
| (イ) | \(R_2+R-r\) | (ロ) | \(\gt\) | (ハ)(5) | \(=\) |
| (ニ) | 4.5 | (ホ)(2) | 21 | (ヘ)(3) | \(R_x(R_2+R-r-R_x)\) |
| (ト) | 2 | (チ)(1) | 9 | (リ) | \(R_x(R_1+R_2+R-r-R_x)\) |
| (ヌ) | \(\lt\) | (ル)(4) | \(\displaystyle \frac{R_2+R-r}{2}\) | (ヲ) | \(\displaystyle \frac{R_1+R_2+R-r}{2}\) |
| (ワ) | 1 | (カ) | 24 | (ヨ) | \(R_x(R_2+R-r)\) |
出典:平成25年度第一種電気主任技術者理論科目A問題問2
解説
電験一種としてはかなり簡単な問題にあたるかと思います。
等価変換後の抵抗\(r\)
図1の電流源を電圧源に等価変換します。
この時3[Ω]の抵抗と6[Ω]の抵抗は直列になるので抵抗\(r\)は3+6=9[Ω]となります。
よって答えは(チ)の9です。
等価変換後の電圧源\(E\)
同様に図1の電流源を電圧源に等価変換します。
\begin{aligned} 7.5 \times 3 &= 22.5 \\ \end{aligned}
この電圧源は1.5[V]の電圧源と向きが逆なので、電圧源\(E\)は22.5-1.5=21[V]となります。
よって答えは(ホ)の21です。
\( R_2\)に流れる電流\(I\)
図2の全体の合成抵抗は
\begin{aligned} R_{total} &=r + R_{\mathrm {x}} + \dfrac{R_{1}\left( R-R_{\mathrm {x}}+R_{2}\right) }{R_{1}+R-R_{\mathrm {x}}+R_{2}} \\ \end{aligned}
全体に流れる電流は
\begin{aligned} I_{total} &=\dfrac{E}{r + R_{\mathrm {x}} + \dfrac{R_{1}\left( R-R_{\mathrm {x}}+R_{2}\right) }{R_{1}+R-R_{\mathrm {x}}+R_{2}}} \\ \end{aligned}
電流\(I\)は、分流の法則より
\begin{aligned} I &=\dfrac{E}{r + R_{\mathrm {x}} + \dfrac{R_{1}\left( R-R_{\mathrm {x}}+R_{2}\right) }{R_{1}+R-R_{\mathrm {x}}+R_{2}}} \cdot \dfrac{R_{1}}{R_{1}+R-R_{\mathrm {x}}+R_{2} } \\ &= \dfrac{R_{1} E}{r\left( R_{1}+R-R_{\mathrm {x}}+R_{2} \right) + R_{\mathrm {x}}\left( R_{1}+R-R_{\mathrm {x}}+R_{2} \right) + R_{1}\left( R-R_{\mathrm {x}}+R_{2}\right)} \\ &= \dfrac{R_{1} E}{R_x(R_2+R-r-R_x) + R_{1}(R_2+R)+r(R_{1}+R_{2}+R) } \\ \end{aligned}
となりますので、答えは(ヘ)の\(R_x(R_2+R-r-R_x)\)です。
分母が最大の場合の\(R_x\)
(3)の分母を\(R_x\)で微分します。
\begin{aligned} f(R_x) &= R_{x}(R_2 + R - r - R_{x}) + R_1(R_2 + R) + r(R_1 + R_2 + R) \\ &= R_x R_2 + R_x R - R_x r - R_x^2 + (R_1 R_2 + R_1 R + r R_1 + r R_2 + r R) \\ \end{aligned}
\begin{aligned} \frac{df}{dR_x} = R_2 + R - r - 2R_x \\ \end{aligned}
これを0とおいて\(R_x\)を求めます。
\begin{aligned} 0 &= R_2 + R - r - 2R_x \\ 2R_x &= R_2 + R - r \\ R_x &= \dfrac{R_2 + R - r}{2} \\ \end{aligned}
よって答えは(ル)の\(\displaystyle \frac{R_2+R-r}{2}\)です。
\((r+R_{x})\)と\((R-R_{x}+R_{2})\)の関係
\((r+R_{x})\)に\(R_x = \dfrac{R_2 + R - r}{2} \)を代入します。
\begin{aligned} r+R_{x} &= r + \dfrac{R_2 + R - r}{2} \\ &= \dfrac{R_2 + R + r}{2} \\ \end{aligned}
同様に、\((R-R_{x}+R_{2})\)に\(R_x = \dfrac{R_2 + R - r}{2} \)を代入します。
\begin{aligned} R-R_{x}+R_{2} &= R- \dfrac{R_2 + R - r}{2} +R_{2} \\ &= \dfrac{R_2 + R + r}{2} \\ \end{aligned}
よって両者は等しく、答えは(ハ)の\(=\)です。
- (1)チ 9
- (2)ホ 21
- (3)ヘ \(R_x(R_2+R-r-R_x)\)
- (4)ル \(\displaystyle \frac{R_2+R-r}{2}\)
- (5)ハ \(=\)