電験一種 H25年 理論 問1
次の文章は,真空中の静電界に関する諸法則の微分形に関する記述である。文中の(0)に当てはまるものを解答群の中から選びなさい。
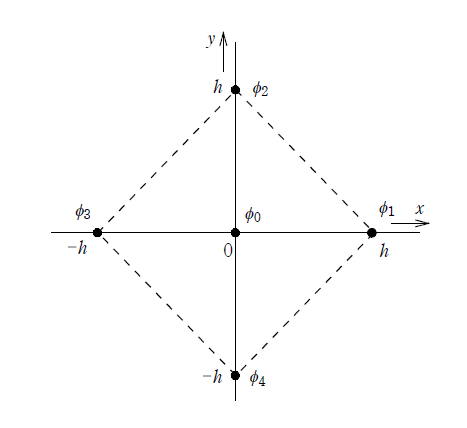
図のように,直交座標系において電界の\(z\)軸成分が零となるような電界について,\(xy\)平面の二次元で電位や電界を考える。ここで,4点\((h, 0), (0, h), (-h, 0), (0, -h)\)の電位がそれぞれ\(\phi_1, \phi_2, \phi_3, \phi_4\)であり,4点を頂点とする正方形の内側には電荷が存在せず,その電位\(\phi\)が次式のような二次関数で表されるとする。
\( \phi(x,y)=ax^2+bxy+cy^2+dx+ey+f \) …①
電界\(\bf{E}\)=\((E_x, E_y, 0)\)は\(\bf{E}\)=-\(\text{grad}\)\(\phi(x, y)\)で計算できる。このとき,電界\(\bf{E}\)について,電界の保存性を表す式より,(1)が常に成り立つ。
また,(2)の法則を微分形で記述すると,電荷が存在しないため,次式となる。
\(\text{div}\bf{E}=\) (3)\(=0\)
この式から導かれる\(a\sim f\)の関係式は,(4) …②
である。
また,①式から原点の電位は,\(\phi_0=\phi(0, 0)=f\)で与えられる。そこで,4点の座標と電位\(\phi_1\sim\phi_4\)を①式に代入し,②式の関係を考慮して,\(f\)を\(\phi_1\sim\phi_4\)を用いて表せば,\(\phi_0=f=\) (5)となる。
| (イ)(1) | \(\rm{rot}\boldsymbol{E}=0\) | (ロ)(4) | \(a+c=0\) | (ハ)(5) | \(\displaystyle \frac{\phi_1+\phi_2+\phi_3+\phi_4}{4}\) | (ニ) | \(\displaystyle \frac{\partial E_y}{\partial x}-\frac{\partial E_x}{\partial y}\) |
| (ホ) | \(d+e=0\) | (ヘ) | \(b^2=4ac\) | (ト) | \(\displaystyle \frac{\partial E_y}{\partial x}+\frac{\partial E_x}{\partial y}\) | (チ)(3) | \(\displaystyle \frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}\) |
| (リ) | \(\displaystyle \frac{\phi_1\phi_3-\phi_2\phi_4}{\phi_1+\phi_2+\phi_3+\phi_4}\) | (ヌ)(2) | ガウス | (ル) | \(\boldsymbol{E}=0\) | (ヲ) | アンペール |
| (ワ) | \(\displaystyle \frac{\phi_1+\phi_2-\phi_3-\phi_4}{2}\) | (カ) | クーロン | (ヨ) | \(\displaystyle \boldsymbol{E}=\left(\frac{\phi_1-\phi_2}{h},\frac{\phi_3-\phi_4}{h},0\right)\) | ||
出典:平成25年度第一種電気主任技術者理論科目A問題問1
解説
マクスウェルの方程式がある程度分かれば後半は難しくない計算問題になりますが、逆に序盤を落とすと全て不正解になる可能性もある問題です。
厳密な内容は専門書を読んでください。とても自分に説明できる内容ではないので。
電界\(\bf{E}\)について成り立つこと
マクスウェル方程式より
\begin{aligned} \nabla \times \boldsymbol{E} &= -\frac{\partial \boldsymbol{B}}{\partial t} \\ \end{aligned}
ここで、この問題においては静電界であることから時間変化がなく右辺が0になるため、
\begin{aligned} \nabla \times \boldsymbol{E} &= 0 \\ \end{aligned}
となります。よって答えは(イ)の\(\rm{rot}\boldsymbol{E}=0\)です。
法則の名前
一種受験者であれば法則名が分からなくても消去法で解けそうな問題です。答えは(ヌ)のガウスです。
ガウスの法則は電気量と電気力線の数の関係を表した法則です。
電荷が存在しないため成り立つ\(\text{div}\bf{E}\)
\(\text{div}\)の定義を知っているか知っていないかだけだと思います。
\begin{aligned} \operatorname{div} \mathbf{A} = \frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z} \\ \end{aligned}
今回電界\(\bf{E}\)は\(z\)の関数ではないので\(\displaystyle \frac{\partial A_z}{\partial z} \)の部分は常に0です。
よって
\begin{aligned} \operatorname{div} \mathbf{E} = \frac{\partial E_x}{\partial x} + \frac{\partial E_y}{\partial y} \\ \end{aligned}
となりますので、答えは(チ)の\(\displaystyle \frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}\)です。
式から導かれる\(a\sim f\)の関係式
まず電界\(\mathbf{E}\)を計算します。
\begin{aligned} \bf{E} &= - \operatorname{grad} \phi \left( x, y \right) \\ &= \left( -2ax -by - d , -bx -2cy -e , 0 \right) \\ \end{aligned}
(3)に従い\(\operatorname{div} \mathbf{E}\)を計算します。
\begin{aligned} \operatorname{div} \mathbf{E} &= \frac{\partial E_x}{\partial x} + \frac{\partial E_y}{\partial y} \\ &= -2a -2c \\ \end{aligned}
問題にある通り、\(\operatorname{div} \mathbf{E}=0\)なので、
\begin{aligned} -2a -2c &= 0 \\ a+c&=0 \end{aligned}
となりますので、答えは(ロ)の\(a+c=0\)です。
原点の電位\(\phi_0=\phi(0, 0)=f\)
問題文にある通り、まずは\(\phi_1\sim\phi_4\)を求めます。
\begin{aligned} \phi_1 &= \phi(h, 0) \\ &= ah^2 + dh + f \\ \end{aligned}
\begin{aligned} \phi_2 &= \phi(0, h) \\ &= ch^2 + eh + f \\ \end{aligned}
\begin{aligned} \phi_3 &= \phi(-h, 0) \\ &= ah^2 - dh + f \\ \end{aligned}
\begin{aligned} \phi_4 &= \phi(0, -h) \\ &= ch^2 - eh + f \\ \end{aligned}
この4つの式から\(f\)を求めます。
\begin{aligned} \phi_1 + \phi_2 + \phi_3 + \phi_4 &= 4f + ah^2 + dh + ch^2 + eh + ah^2 - dh +ch^2 - eh \\ \phi_1 + \phi_2 + \phi_3 + \phi_4 &= 4f + \left(2a + 2c\right)h^2 \\ \end{aligned}
(4)より、上式の括弧の中身は0となるので
\begin{aligned} 4f &= \phi_1 + \phi_2 + \phi_3 + \phi_4 \\ f &= \dfrac{\phi_1 + \phi_2 + \phi_3 + \phi_4 }{4} \\ \end{aligned}
となります。よって答えは(ハ)の\(\displaystyle \frac{\phi_1+\phi_2+\phi_3+\phi_4}{4}\)です。
- (1)イ \(\rm{rot}\boldsymbol{E}=0\)
- (2)ヌ ガウス
- (3)チ \(\displaystyle \frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}\)
- (4)ロ \(a+c=0\)
- (5)ハ \(\displaystyle \frac{\phi_1+\phi_2+\phi_3+\phi_4}{4}\)