電験一種 H24年 理論 問3
次の文章は、分布定数回路に関する記述である。文中の(0)に当てはまるものを解答群の中から選びなさい。
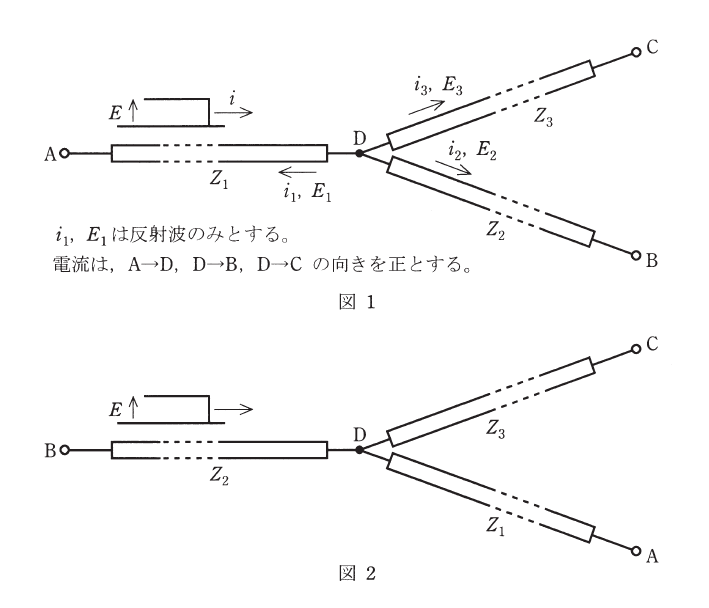
図のように、特性インピーダンスがそれぞれ\(Z_{1}\)、\(Z_{2}\)、\(Z_{3}\)の3本の無損失線路が接続されている。\(Z_{1}\)と\(Z_{2}\)、\(Z_{3}\)の関係を求めたい。線路間に電気的・磁気的結合はなく、また、A, B, Cそれぞれの端子では反射がないものとする。
A, Bそれぞれの端子から接続点Dに向かって波頭が階段状で波高値\(E\)の電圧波が進入したとき、以下の現象が見られた。
(a) 図1のようにA端子のみから電圧波が進入したとき、接続点Dで反射が生じた。
(b) 図2のようにB端子のみから電圧波が進入したとき、接続点Dでは反射が生じなかった。
現象(a)に対して、A端子からの入射波による電流\(i\)、接続点Dでの反射により生じる電圧\(E_{1}\)、電流\(i_{1}\)、また、\(Z_{2}\)側、\(Z_{3}\)側への透過波による電圧\(E_{2}\)、電流\(i_{2}\)、電圧\(E_{3}\)、電流\(i_{3}\)を図のようにとる。電流は入射波が接続点Dに向かって進行する方向及び透過波が接続点Dから離れる方向を正とする。
接続点Dの電圧、電流の関係はそれぞれ次式で表される。
\( \left. \begin{array}{l} E+E_{1}=E_{2}=E_{3} \\ i+i_{1}=i_{2}+i_{3} \\ \end{array} \quad \right\} \quad \cdots \cdots \cdots \text {①} \)
ここで、\(Y_{1}=\dfrac{1}{Z_{1}}, Y_{2}=\dfrac{1}{Z_{2}}, Y_{3}=\dfrac{1}{Z_{3}} \)とおき、それらを用いて\(E_{1}\)、\(E_{2}\)と\(E\)の関係を表すと、次のようになる。
\( \left. \begin{array}{l} E_{1} = \boxed{\vphantom{2}\hspace{1em} \text{(1)} \vphantom{2} \hspace{1em}} \times E \\ E_{2} = \boxed{\vphantom{2}\hspace{1em} \text{(2)} \vphantom{2} \hspace{1em}} \times E \end{array} \quad \right\} \quad \cdots \cdots \cdots \text {②} \)
次に現象(b)について考える。接続点Dで反射が生じないことから、\(Y_{2}\)は\(Y_{1}\)と\(Y_{3}\)を用いると次式で表される。
\( Y_{2} = \boxed{\vphantom{2}\hspace{1em} \text{(3)} \vphantom{2} \hspace{1em}} \quad \cdots \cdots \cdots \text {③} \)
現象(a)において反射が生じたときの接続点Dの電位が\(\dfrac{2}{3}E\)であったとき、\(Z_{2}\)、\(Z_{3}\)と\(Z_{1}\)の関係は次のようになる。
\( \left. \begin{array}{l} Z_{2} = \boxed{\vphantom{2}\hspace{1em} \text{(4)} \vphantom{2} \hspace{1em}} \\ Z_{3} = \boxed{\vphantom{2}\hspace{1em} \text{(5)} \vphantom{2} \hspace{1em}} \\ \end{array} \quad \right\} \quad \cdots \cdots \cdots \text {④} \)
| (イ) | \(\displaystyle \frac{1}{2}Z_1\) | (ロ) | \(\displaystyle \frac{Y_1+Y_3}{Y_1Y_3}\) | (ハ)(5) | \(2Z_1\) |
| (ニ) | \(\displaystyle \frac{Y_1+Y_2+Y_3}{Y_1-Y_2-Y_3}\) | (ホ)(2) | \(\displaystyle \frac{2Y_1}{Y_1+Y_2+Y_3}\) | (ヘ) | \(\displaystyle \frac{3}{2}Z_1\) |
| (ト) | \(\displaystyle \frac{Y_1Y_3}{Y_1+Y_3}\) | (チ) | \(\displaystyle \frac{2Y_1}{Y_1-Y_2-Y_3}\) | (リ)(3) | \(Y_1+Y_3\) |
| (ヌ) | \(\displaystyle \frac{1}{\sqrt{2}}Z_1\) | (ル)(1) | \(\displaystyle \frac{Y_1-Y_2-Y_3}{Y_1+Y_2+Y_3}\) | (ヲ) | \(3Z_1\) |
| (ワ) | \(\displaystyle \frac{2Y_2Y_3}{Y_1Y_2+Y_2Y_3+Y_3Y_1}\) | (カ)(4) | \(\displaystyle \frac{2}{3}Z_1\) | (ヨ) | \(\displaystyle \frac{Y_2Y_3-Y_1(Y_2+Y_3)}{Y_1Y_2+Y_2Y_3+Y_3Y_1}\) |
出典:平成24年度第一種電気主任技術者理論科目A問題問3
解説
二次試験でも必要となる知識が含まれている問題です。
電圧と電流の関係が問題では示されていますが、二次試験では与えられないと考えられるためここから理解しておきたいです。
\(E_{1}\)と\(E\)の関係
まずは以下の関係式を抑えます。
\begin{aligned} E &= Z_1 i \\ E_1 &= -Z_1 i_1 \\ E_2 &= Z_2 i_2 \\ E_3 &= Z_3 i_3 \\ \end{aligned}
ここで、電流はAからDが正なので\(i_1\)は負になることに注意が必要です。
上記の関係式を問題にあるアドミタンスを用いて表現します。
\begin{aligned} i &= Y_1 E \\ i_1 &= -Y_1 E_1\\ i_2 &= Y_2 E_2 \\ i_3 &= Y_3 E_3 \\ \end{aligned}
これを問題にある電流の式に代入します。
\begin{aligned} i+i_{1} &=i_{2}+i_{3} \\ Y_1 E -Y_1 E_1 &= Y_2 E_2 + Y_3 E_3 \\ \end{aligned}
ここで\(E+E_{1}=E_{2}=E_{3}\)なので
\begin{aligned} Y_1 E -Y_1 E_1 &= Y_2 \left( E+E_{1} \right) + Y_3 \left( E+E_{1} \right) \\ \end{aligned}
となります。これを整理します。
\begin{aligned} Y_1 E -Y_1 E_1 &= Y_2 \left( E+E_{1} \right) + Y_3 \left( E+E_{1} \right) \\ Y_1 E -Y_1 E_1 &= Y_2E + Y_2E_{1} + Y_3E + E_{1} \\ \left( -Y_1 -Y_2 -Y_3 \right)E_{1} &= \left( -Y_1 + Y_2 + Y_3 \right) E \\ E_1 &= \dfrac{-Y_1 + Y_2 + Y_3}{-Y_1 - Y_2 - Y_3} E \\ E_1 &= \dfrac{Y_1 - Y_2 - Y_3}{Y_1 + Y_2 + Y_3} E \\ \end{aligned}
となりますので、答えは(ル)の\(\displaystyle \frac{Y_1-Y_2-Y_3}{Y_1+Y_2+Y_3}\)です。
\(E_{2}\)と\(E\)の関係
\(E+E_{1}=E_{2}\)なので、ここに(1)の\(E_1\)を代入します。
\begin{aligned} E+E_{1} &=E_{2} \\ E+\dfrac{Y_1 - Y_2 - Y_3}{Y_1 + Y_2 + Y_3} E &=E_{2} \\ \dfrac{Y_1 + Y_2 + Y_3}{Y_1 + Y_2 + Y_3} E+\dfrac{Y_1 - Y_2 - Y_3}{Y_1 + Y_2 + Y_3} E &=E_{2} \\ \dfrac{2Y_1}{Y_1 + Y_2 + Y_3} E &=E_{2} \\ E_{2} &= \dfrac{2Y_1}{Y_1 + Y_2 + Y_3} E\\ \end{aligned}
よって答えは(ホ)の\(\displaystyle \frac{2Y_1}{Y_1+Y_2+Y_3}\)です。
\(Y_{2}\)を\(Y_{1}\)と\(Y_{3}\)を用いて表す
(b)の時、接続点Dで反射が生じなかったということはB-Dの特性インピーダンスとDから右を見た時のインピーダンスが等しいということなので
\begin{aligned} Z_2 &= \dfrac{Z_3 Z_1}{Z_3 + Z_1} \\ \end{aligned}
が成り立ちます。これをアドミタンスを用い表して\(Y_2\)を求めます。
\begin{aligned} Z_2 &= \dfrac{Z_3 Z_1}{Z_3 + Z_1} \\ \dfrac{1}{Y_2} &= \dfrac{\dfrac{1}{Y_3} \cdot \dfrac{1}{Y_1}}{\dfrac{1}{Y_3} + \dfrac{1}{Y_1}} \\ \end{aligned}
\begin{aligned} Y_2 &= \dfrac{\dfrac{1}{Y_3} + \dfrac{1}{Y_1}}{\dfrac{1}{Y_3} \cdot \dfrac{1}{Y_1}} \\ &= Y_1 + Y_3 \\ \end{aligned}
よって答えは(リ)の\(Y_1+Y_3\)です。
\(Z_2\)と\(Z_1\)の関係
(2)から求めてもいいですが、ここでは電圧反射係数から求めたいと思います。
接続点Dの電位が\(\dfrac{2}{3} E\)ということは、電圧反射係数が\(-\dfrac{1}{3}\)ということです。
よって、以下が成り立ちます。
\begin{aligned} -\dfrac{1}{3} &= \dfrac{\dfrac{Z_3 Z_2}{Z_3 + Z_2} - Z_1}{\dfrac{Z_3 Z_2}{Z_3 + Z_2} + Z_1 } \\ \end{aligned}
これを整理します。
\begin{aligned} -\dfrac{1}{3} &= \dfrac{\dfrac{Z_3 Z_2}{Z_3 + Z_2} - Z_1}{\dfrac{Z_3 Z_2}{Z_3 + Z_2} + Z_1 } \\ -\dfrac{Z_3 Z_2}{Z_3 + Z_2} - Z_1 &= 3 \left(\dfrac{Z_3 Z_2}{Z_3 + Z_2} - Z_1 \right) \\ -Z_1 Z_2 - Z_2 Z_3 - Z_3 Z_1 &= 3\left(-Z_1 Z_2 + Z_2 Z_3 - Z_3 Z_1 \right) \\ 2Z_1 Z_2 - 4Z_2 Z_3 + 2Z_3 Z_1 &= 0 \\ Z_1 Z_2 - 2Z_2 Z_3 + Z_3 Z_1 &= 0 \\ \end{aligned}
問題では\(Z_2\)と\(Z_1\)の関係を問われていますので、\(Z_3\)を消去します。
上の式を\(Z_3=\)の形にします。
\begin{aligned} Z_1 Z_2 - 2Z_2 Z_3 + Z_3 Z_1 &= 0 \\ Z_3 \left( 2Z_2 - Z_1 \right) &= Z_1 Z_2 \\ Z_3 &= \dfrac{Z_1 Z_2}{2Z_2 - Z_1} \\ \end{aligned}
(3)ででてきた\(Z_2 = \dfrac{Z_3 Z_1}{Z_3 + Z_1}\)に代入します。
\begin{aligned} Z_2 &= \dfrac{Z_3 Z_1}{Z_3 + Z_1} \\ &= \dfrac{\dfrac{Z_1 Z_2}{2Z_2 - Z_1} \cdot Z_1}{\dfrac{Z_1 Z_2}{2Z_2 - Z_1} + Z_1} \\ \end{aligned}
\begin{aligned} 1 &= \dfrac{\dfrac{Z_1}{2Z_2 - Z_1} }{\dfrac{ Z_2}{2Z_2 - Z_1} + 1 } \\ &= \dfrac{Z_1}{Z_2 + 2Z_2 - Z_1 } \\ \end{aligned}
\begin{aligned} Z_2 + 2Z_2 -Z_1 &= Z_1 \\ 2Z_2 &= 2Z_1 \\ Z_2 &= \dfrac{2}{3} Z_1 \\ \end{aligned}
よって答えは(カ)の\(\displaystyle \frac{2}{3}Z_1\)です。
\(Z_3\)と\(Z_1\)の関係
\(Z_3 = \dfrac{Z_1 Z_2}{2Z_2 - Z_1}\)に(4)の\(Z_2 = \dfrac{2}{3} Z_1\)を代入します。
\begin{aligned} Z_3 &= \dfrac{Z_1 Z_2}{2Z_2 - Z_1} \\ &= \dfrac{Z_1 \cdot \dfrac{2}{3}Z_1}{2 \cdot \dfrac{2}{3}Z_1 - Z_1} \\ &= \dfrac{2Z_1}{4 - 3} \\ &= 2Z_1 \\ \end{aligned}
よって答えは(ハ)の\(2Z_1\)です。
- (1)ル \(\displaystyle \frac{Y_1-Y_2-Y_3}{Y_1+Y_2+Y_3}\)
- (2)ホ \(\displaystyle \frac{2Y_1}{Y_1+Y_2+Y_3}\)
- (3)リ \(Y_1+Y_3\)
- (4)カ \(\displaystyle \frac{2}{3}Z_1\)
- (5)ハ \(2Z_1\)