電験一種 H24年 理論 問2
次の文章は、直流回路に関する記述である。文中の(0)に当てはまる最も近いものを解答群の中から選びなさい。
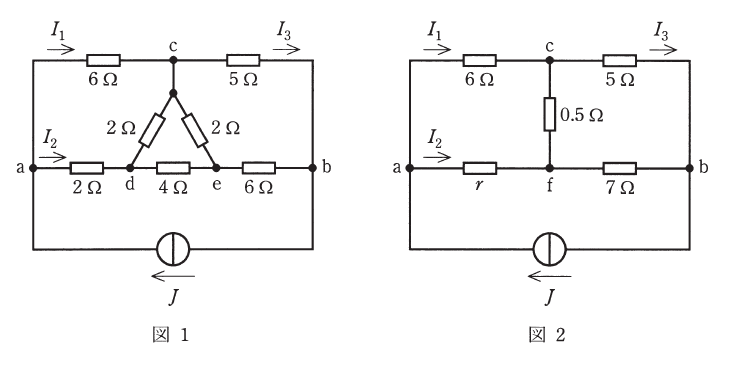
図1及び図2において、電流源の電流を \(J\) とする。いま、図1の端子 cde からなる\(\triangle\)接続をY接続に変換すると図2のように表され、\(r\) は(1) \([\Omega]\) となる。
次に、図2の端子 bcf からなる\(\triangle\)接続をY接続に変換して \(I_{1}\) 及び \(I_{2}\) を求めれば、\(I_{1} =\)(2) \(\times J\)、\(I_{2} =\)(3) \(\times J\) となる。
一方、図2の経路 acb と afb の電圧降下は等しいことから、\(I_{3}\) は \(I_{3} =\)(4) \(\times J\) となる。また、端子 a-b 間の電圧 \(V_{ab}\) は、\(V_{ab} =\)(5) \(\times J\) となる。
| (イ) | 0.271 | (ロ)(2) | 0.346 | (ハ) | 0.355 | (ニ) | 0.548 |
| (ホ)(4) | 0.574 | (ヘ) | 0.630 | (ト) | 0.645 | (チ)(3) | 0.654 |
| (リ) | 0.728 | (ヌ) | 1 | (ル) | 2.59 | (ヲ)(1) | 3 |
| (ワ) | 4 | (カ) | 4.87 | (ヨ)(5) | 4.95 |
出典:平成24年度第一種電気主任技術者理論科目A問題問2
解説
Δ-Y変換を覚えていれば難しい問題ではないですが、数字が細かいので冷静に解きたいところです。
Δ-Y変換後の\(r\)
Δ-Y変換して元からある2[Ω]の抵抗と足し合わせます。
右側の抵抗が6[Ω]→7[Ω]になっているあたり、Δ-Y変換後の抵抗が1[Ω]になるであろうというのは想像つくかもしれませんが、念のため計算します。
\begin{aligned} \dfrac{2 \times 4}{2+ 4+ 2} &=\dfrac{8}{8} \\ &= 1 \\ \end{aligned}
よって
\begin{aligned} r &= 2 + 1 \\ &= 3 \\ \end{aligned}
となりますので、答えは(ヲ)の3です。
\(I_1\)を求める
問題の通り端子bcfをΔ-Y変換するのが楽かと思いますが、参考書に当然書いてあるやり方なのでここでは別の解き方でやります。
本番ではΔ-Y変換で解くべきかと思います。
3つの方程式を立てそこから求めます。
電流源の電流\(J\)は\(I_1\)と\(I_2\)に分流するので
\begin{aligned} I_1 + I_2 &= J \\ \end{aligned}
です。
経路acbとafbの電圧降下は等しいので
\begin{aligned} 6I_1 + 5I_3 &= 3I_2 + 7\left(I_1 + I_2 - I_3\right) \\ -I_1 - 10I_2 +12I_3 &= 0 \\ \end{aligned}
が成り立ちます。
acfを一周するとキルヒホッフの第2法則により電圧降下は0です。よって
\begin{aligned} 6I_1 + 0.5\left(I_1 - I_3 \right) -3I_2 &= 0 \\ 6.5I_1 -3I_2 -0.5I_3 &= 0 \\ 13 I_1 -6I_2 - I_3 &= 0 \\ \end{aligned}
が成り立ちます。これらをまとめると
\begin{aligned} \begin{pmatrix} 1 & 1 & 0 \\ -1 & -10 & 12 \\ 13 & -6 & -1 \end{pmatrix} \begin{pmatrix} I_1 \\ I_2 \\ I_3 \end{pmatrix} = \begin{pmatrix} J \\ 0 \\ 0 \end{pmatrix} \end{aligned}
となるので、後はこれをクラメルの公式を使って解きます。
\begin{aligned} A &= \begin{pmatrix} 1 & 1 & 0 \\ -1 & -10 & 12 \\ 13 & -6 & -1 \end{pmatrix} \\ \mathbf{b} &= \begin{pmatrix} J \\ 0 \\ 0 \end{pmatrix} \end{aligned}
とします。
まずは\(\det(A)\)を計算します。
\begin{aligned} \det(A) &= 10 + 156 - \left(-72 + 1 \right) \\ &= 237 \\ \end{aligned}
\(A_1\) は\(A\)の第1列を\(\mathbf{b}\)で置き換えた行列です。
\begin{aligned} A_1 = \begin{pmatrix} J & 1 & 0 \\ 0 & -10 & 12 \\ 0 & -6 & -1 \end{pmatrix} \end{aligned}
\begin{aligned} \det(A_1) &= J \cdot \det \begin{pmatrix} -10 & 12 \\ -6 & -1 \end{pmatrix} \\ &= J \left( (-10)(-1) - (12)(-6) \right) \\ &= 82 J \\ \end{aligned}
\begin{aligned} I_1 &= \frac{\det(A_1)}{\det(A)} \\ &= \frac{82 }{237} J \\ &\fallingdotseq 0.346J \\ \end{aligned}
よって(2)の答えは(ロ)の0.346です。
\(I_2\)を求める
同様に(3)も考えます。
\(A_2\) は\(A\)の第2列を\(\mathbf{b}\)で置き換えた行列です。
\begin{aligned} A_2 = \begin{pmatrix} 1 & J & 0 \\ -1 & 0 & 12 \\ 13 & 0 & -1 \end{pmatrix} \end{aligned}
\begin{aligned} \det(A_2) &= -J \cdot \det \begin{pmatrix} -1 & 12 \\ 13 & -1 \end{pmatrix} \\ &= -J \left( (-1)(-1) - (12)(13) \right) \\ &= 155 J \\ \end{aligned}
\begin{aligned} I_2 &= \frac{\det(A_2)}{\det(A)} \\ &= \frac{155 }{237}J \\ &\fallingdotseq 0.654J \\ \end{aligned}
よって(3)の答えは(チ)の0.654です。
\(I_3\)を求める
同様に(4)も考えます。
\(A_3\) は\(A\)の第3列を\(\mathbf{b}\)で置き換えた行列です。
\begin{aligned} A_3 = \begin{pmatrix} 1 & 1 & J \\ -1 & -10 & 0 \\ 13 & -6 & 0 \end{pmatrix} \end{aligned}
\begin{aligned} \det(A_3) &= J \cdot \det \begin{pmatrix} -1 & -10 \\ 13 & -6 \end{pmatrix} \\ &= J \left( (-1)(-6) - (-10)(13) \right) \\ &= 136 J \\ \end{aligned}
\begin{aligned} I_3 &= \frac{\det(A_3)}{\det(A)} \\ &= \frac{136 }{237}J \\ &\fallingdotseq 0.574J \\ \end{aligned}
よって(4)の答えは(ホ)の0.574です。
端子a-b間の電圧\(V_{ab}\)
\(I_1\)、\(I_3\)が分かっているので経路acbの電圧降下を計算します。
\begin{aligned} V_{ab} &= 6I_1 + 5I_3 \\ &= 6 \times 0.346J + 5 \times 0.574J \\ &= 4.946J \\ &\fallingdotseq 4.95J \\ \end{aligned}
よって答えは(ヨ)の4.95です。
- (1)ヲ 3
- (2)ロ 0.346
- (3)チ 0.654
- (4)ホ 0.574
- (5)ヨ 4.95