電験一種 H24年 理論 問1
次の文章は、線電荷周囲の電界に関する記述である。文中の(0)に当てはまるものを解答群の中から選びなさい。ただし、空間の誘電率は \(\varepsilon_0\) とし、各図は断面図である。
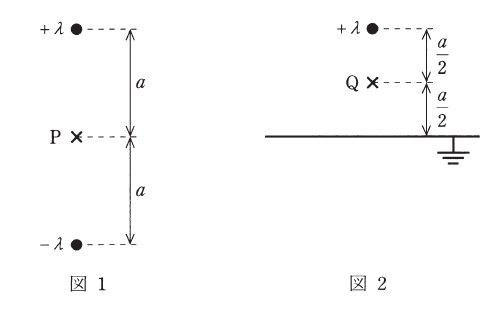
図1のように、線電荷密度の大きさが \(\lambda\) であり、極性が異なる2本の無限長線電荷が互いに平行に距離 \(2a\) を隔てて置かれている場合、中間点Pでの電界の大きさは(1)である。またこのとき、線電荷に生じる単位長さ当たりの力の大きさは(2)となる。
次に、図2のように、線電荷密度が \(\lambda\) である無限長線電荷が、接地平面と平行に距離 \(a\) を隔てて置かれている場合を考える。このとき、電界の境界条件より、接地面には電気力線が面に垂直に入射することに留意して、影像線電荷を考えると、線電荷と接地面との中間点Qでの電界の大きさは(3)と求めることができる。
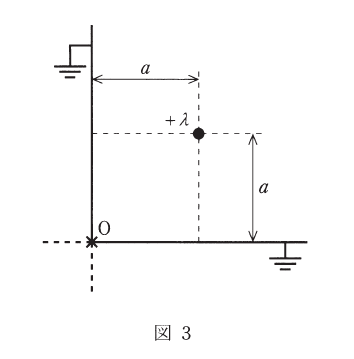
さらに、図3のように直交する2枚の接地平面があり、両平面と平行に距離 \(a\) を隔てて、線電荷密度が \(\lambda\) である無限長線電荷が置かれている。この場合、電界の境界条件を考えると、点 \(O\) における電界の大きさは(4)になる。この場合の境界条件を満たす影像線電荷を考えると、線電荷に生じる単位長さ当たりの力の大きさは(5)と求めることができる。
| (イ) | \(\displaystyle \frac{2\lambda}{3\pi\varepsilon_0a}\) | (ロ)(1) | \(\displaystyle \frac{\lambda}{\pi\varepsilon_0a}\) | (ハ) | \(\displaystyle \frac{3\lambda}{4\pi\varepsilon_0a}\) |
| (ニ)(5) | \(\displaystyle \frac{\sqrt{2}\lambda^2}{8\pi\varepsilon_0a}\) | (ホ) | \(\displaystyle \frac{\sqrt{2}\lambda^2}{4\pi\varepsilon_0a}\) | (ヘ) | \(\displaystyle \frac{\sqrt{2}\lambda}{2\pi\varepsilon_0a}\) |
| (ト) | \(\displaystyle \frac{\lambda^2}{2\pi\varepsilon_0a}\) | (チ) | \(\displaystyle \frac{\sqrt{2}\lambda}{2\pi\varepsilon_0a}\) | (リ)(3) | \(\displaystyle \frac{4\lambda}{3\pi\varepsilon_0a}\) |
| (ヌ) | \(\displaystyle \frac{\lambda}{4\pi\varepsilon_0a}\) | (ル) | \(\displaystyle \frac{\lambda^2}{8\pi\varepsilon_0a}\) | (ヲ)(4) | \(0\) |
| (ワ) | \(\displaystyle \frac{\sqrt{2}\lambda}{4\pi\varepsilon_0a}\) | (カ)(2) | \(\displaystyle \frac{\lambda^2}{4\pi\varepsilon_0a}\) | (ヨ) | \(\displaystyle \frac{\lambda}{2\pi\varepsilon_0a}\) |
出典:平成24年度第一種電気主任技術者理論科目A問題問1
解説
電気影像法の問題です。
無限長線電荷による単位長さあたりの電界\(E\)は\(E = \dfrac{\lambda}{2\pi\varepsilon r}\)です。\(\lambda\)は線電荷密度、\(\varepsilon\)は誘電率です。
中間点Pでの電界の大きさ
各線電荷による中間点\(P\)電界の大きさはどちらも\(\dfrac{\lambda}{2\pi\varepsilon_0 a}\)です。
また、その方向は上の\(+\lambda\)による電界は下向き、下の\(-\lambda\)による電界もまた下向きなので中間点\(P\)の電界の大きさ\(E_P\)はこれらの和になります。よって
\begin{aligned} E_P &= \dfrac{\lambda}{2\pi\varepsilon_0 a} + \dfrac{\lambda}{2\pi\varepsilon_0 a} \\ &= \dfrac{\lambda}{\pi\varepsilon_0 a} \\ \end{aligned}
となりますので、答えは(ロ)の\(\displaystyle \frac{\lambda}{\pi\varepsilon_0a}\)です。
線電荷に生じる単位長さ当たりの力の大きさ
\(+\lambda\)による下の線電荷の位置の電界\(E\)は、距離が\(2a\)なので
\begin{aligned} E &= \dfrac{\lambda}{2\pi\varepsilon_0 \cdot 2a} \\ &= \dfrac{\lambda}{4\pi\varepsilon_0 a} \end{aligned}
です。線電荷に生じる単位長さ当たりの力の大きさ\(F\)は、これと線電荷密度の積なので
\begin{aligned} F &= \lambda E\\ &= \dfrac{\lambda^2 }{4\pi\varepsilon_0 a} \\ \end{aligned}
です。よって答えは(カ)の\(\displaystyle \frac{\lambda^2}{4\pi\varepsilon_0a}\)です。
なお、向きは引き合う方向なので上向きです。
線電荷と接地面との中間点Qでの電界の大きさ
電気影像法で考えると、図2では接地平面より下に\(a\)の位置に\(-\lambda\)の線電荷があるとみなせます。
よって中間点\(Q\)の電界\(E_Q\)は、線電荷\(+\lambda\)から中間点\(Q\)の距離は\(\dfrac{a}{2}\)、線電荷\(-\lambda\)から中間点\(Q\)の距離は\(\dfrac{3a}{2}\)になることに注意して
\begin{aligned} E_F &= \dfrac{\lambda}{2\pi\varepsilon_0 \cdot \dfrac{a}{2}} + \dfrac{\lambda}{2\pi\varepsilon_0 \cdot \dfrac{3a}{2}} \\ &= \dfrac{3\lambda}{3\pi\varepsilon_0 a} + \dfrac{\lambda}{3\pi\varepsilon_0 a} \\ &= \dfrac{4\lambda}{3\pi\varepsilon_0 a} \\ \end{aligned}
となります。よって答えは(リ)の\(\displaystyle \frac{4\lambda}{3\pi\varepsilon_0a}\)です。
点\(O\)における電界の大きさ
同様に考えると、線電荷\(+\lambda\)の位置を\((a,a)\)とした時に線電荷\(-\lambda\)が\((-a,a)\)と\((a,-a)\)に必要です。
しかし、これでは例えば左側に置いた線電荷\(-\lambda\)によって下側の接地平面の電位が乱れます。下側に置いた線電荷\(-\lambda\)も左側の接地平面の電位を乱します。よって更に仮想電荷が必要になります。
これらを同時に打ち消すためには、\((-a,-a)\)に仮想電荷があればよく、それは\(-\lambda\)とは逆の電荷なので\(+\lambda\)となります。
これを基に点\(O\)の電界を求めます。
点\(O\)との距離はいずれも\(\sqrt{2}a\)であることから電界の大きさは等しいので、後は向きに気を付けて足し合わせます。
点\(O\)を挟んで反対に同符号の線電荷がある形になるので、電界の向きはそれぞれ反対となりそれらを足し合わせると0になります。
よって答えは(ヲ)の\(0\)です。
線電荷に生じる単位長さ当たりの力の大きさ
力の向きに注意して足し合わせます。
\(-\lambda\)の線電荷による電界によりかかる力\(F_1\)と\(F_2\)は距離が\(2a\)なので
\begin{aligned} F_1 = F_2 &= \lambda \cdot \dfrac{\lambda }{2\pi\varepsilon_0 \cdot 2a} \\ &= \dfrac{\lambda^2 }{4\pi\varepsilon_0 a} \\ \end{aligned}
です。向きはそれぞれ左方向と下方向です。
同様に、
\(+\lambda\)の線電荷による電界によりかかる力\(F_3\)は距離が\(2\sqrt{2}a\)なので
\begin{aligned} F_3 &= \lambda \cdot \dfrac{\lambda}{2\pi\varepsilon_0 \cdot 2 \sqrt{2}a} \\ &= \dfrac{\lambda^2 }{4\sqrt{2} \pi\varepsilon_0 a} \\ \end{aligned}
です。向きは右上方向です。
これらの力の合成\(F_4\)は
\begin{aligned} F_4 &= F_1 \cos \dfrac{\pi}{4} + F_2 \cos \dfrac{\pi}{4} - F_3 \\ &= \dfrac{\lambda^2 }{4\sqrt{2} \pi\varepsilon_0 a} + \dfrac{\lambda^2 }{4\sqrt{2} \pi\varepsilon_0 a} - \dfrac{\lambda^2 }{4\sqrt{2} \pi\varepsilon_0 a}\\ &= \dfrac{\lambda^2 }{4\sqrt{2} \pi\varepsilon_0 a} \\ &= \dfrac{\sqrt{2} \lambda^2 }{8 \pi\varepsilon_0 a} \end{aligned}
となりますので、答えは(ニ)の\(\displaystyle \frac{\sqrt{2}\lambda^2}{8\pi\varepsilon_0a}\)です。
- (1)ロ \(\displaystyle \frac{\lambda}{\pi\varepsilon_0a}\)
- (2)カ \(\displaystyle \frac{\lambda^2}{4\pi\varepsilon_0a}\)
- (3)リ \(\displaystyle \frac{4\lambda}{3\pi\varepsilon_0a}\)
- (4)ヲ \(0\)
- (5)ニ \(\displaystyle \frac{\sqrt{2}\lambda^2}{8\pi\varepsilon_0a}\)